Question 111423: I am having trouble with all five of these quadratic equations PLEASE HELP!
1. 
2. 
3. 
4. 
5. 
Any help would be greatly appreciated. I am going to continue working on these problems. They are due today by 4:30 p.m. est.
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! #1
^2=36) Start with the given equation Start with the given equation
 Divide both sides by 9 Divide both sides by 9
 Take the square root of both sides Take the square root of both sides
 Simplify the square root (note: If you need help with simplifying the square root, check out this solver) Simplify the square root (note: If you need help with simplifying the square root, check out this solver)
 Add 8 to both sides to isolate x. Add 8 to both sides to isolate x.
Break down the expression into two parts:
 or or 
Now combine like terms for each expression:
 or or 
-----------------------------------
Answer:
So our solution is
 or or 
Notice when we graph the equations  and and  we get: we get:
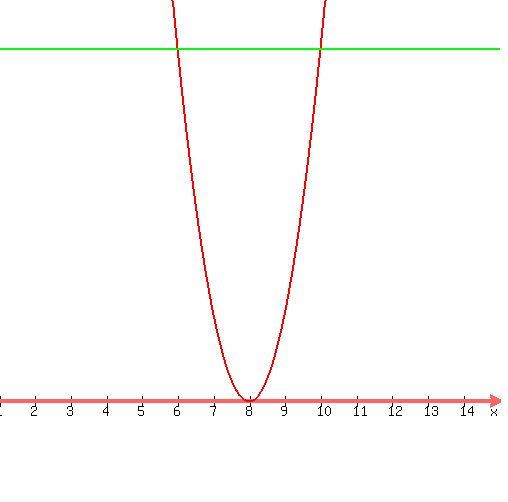 graph of graph of  (red) and (red) and  (green) (green)
Here we can see that the two equations intersect at x values of  and and  , so this verifies our answer. , so this verifies our answer.
#2
| Solved by pluggable solver: Quadratic Formula |
Let's use the quadratic formula to solve for x:
Starting with the general quadratic

the general solution using the quadratic equation is:

So lets solve  (note: since the polynomial does not have an "x" term, the 2nd coefficient is zero. In other words, b=0. So that means the polynomial really looks like (note: since the polynomial does not have an "x" term, the 2nd coefficient is zero. In other words, b=0. So that means the polynomial really looks like  notice notice  , ,  , and , and  ) )
 Plug in a=27, b=0, and c=-49 Plug in a=27, b=0, and c=-49
 Square 0 to get 0 Square 0 to get 0
 Multiply Multiply 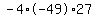 to get to get 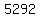
 Combine like terms in the radicand (everything under the square root) Combine like terms in the radicand (everything under the square root)
 Simplify the square root (note: If you need help with simplifying the square root, check out this solver) Simplify the square root (note: If you need help with simplifying the square root, check out this solver)
 Multiply 2 and 27 to get 54 Multiply 2 and 27 to get 54
So now the expression breaks down into two parts
 or or 
Now break up the fraction
 or or 
Simplify
 or or 
So the solutions are:
 or or 
|
#3
 Start with the given equation Start with the given equation
 Add Add  to both sides to both sides
 Factor the left side (note: if you need help with factoring, check out this solver) Factor the left side (note: if you need help with factoring, check out this solver)
Now set each factor equal to zero:
 or or 
 or or  Now solve for x in each case Now solve for x in each case
So our solutions are  or or 
Notice if we graph  we get we get
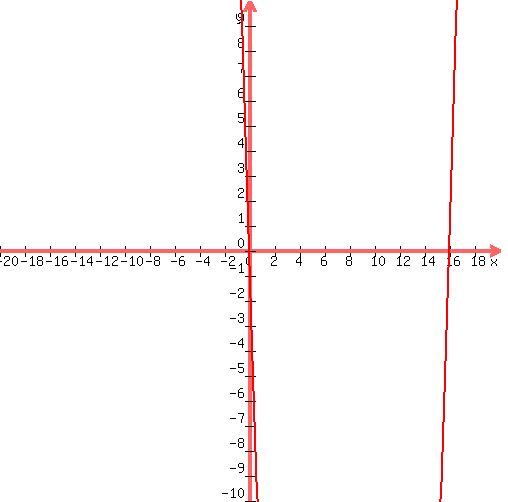
and we can see that the graph has roots at  or or  , so this verifies our answer. , so this verifies our answer.
#4
 Start with the given expression Start with the given expression
 Factor out the GCF Factor out the GCF 
 Factor the inner expression Factor the inner expression 
Now set each factor equal to zero:
 , ,  or or 
 , ,  , or , or  Now solve for x in each case Now solve for x in each case
Notice we get the solution  twice twice
So our solutions are  or or 
Notice if we graph  we get we get

and we can see that the graph has roots at  and and  so this verifies our answer. so this verifies our answer.
#5
| Solved by pluggable solver: Quadratic Formula |
Let's use the quadratic formula to solve for x:
Starting with the general quadratic

the general solution using the quadratic equation is:

So lets solve  (note: since the polynomial does not have an "x" term, the 2nd coefficient is zero. In other words, b=0. So that means the polynomial really looks like (note: since the polynomial does not have an "x" term, the 2nd coefficient is zero. In other words, b=0. So that means the polynomial really looks like  notice notice  , ,  , and , and  ) )
 Plug in a=1, b=0, and c=69 Plug in a=1, b=0, and c=69
 Square 0 to get 0 Square 0 to get 0
 Multiply Multiply 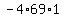 to get to get 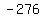
 Combine like terms in the radicand (everything under the square root) Combine like terms in the radicand (everything under the square root)
 Simplify the square root (note: If you need help with simplifying the square root, check out this solver) Simplify the square root (note: If you need help with simplifying the square root, check out this solver)
 Multiply 2 and 1 to get 2 Multiply 2 and 1 to get 2
After simplifying, the quadratic has roots of
 or or 
|
|
|
|