Question 1111308: The difference of two positive numbers is six. Their product is 223 less than the sum of their squares. What are the two numbers?
Found 3 solutions by josgarithmetic, ikleyn, TeachMath:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
Answer by ikleyn(52779)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let x be the larger number, y be the lesser number.
Then
x - y = 6, (1)
xy = x^2 + y^2 - 223. (2)
Square equation (1) (both sides). Keep equation (2) as is:
x^2 - 2xy + y^2 = 36, (3)
x^2 - xy + y^2 = 223 (4) (<<<---=== it is transformed eq(2) )
----------------------------------Subtract eq(3) from eq(4). You will get
xy = 187.
Now you have system of two equations
x - y = 6,
xy = 187.
It is reduced to the quadratic equation
x*(x-6) = 187
x^2 -6x - 187 = 0
 = =  = =  , ,
 = = 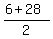 = 17, = 17,  = 11. = 11.
 = =  = -11, = -11,  = -17.
Answer. There are TWO solutions: a) (x,y) = (17,11); b) (x,y) = (-11,-17).
Since the problem asks about positive numbers, only first pair satisfies this requirement. = -17.
Answer. There are TWO solutions: a) (x,y) = (17,11); b) (x,y) = (-11,-17).
Since the problem asks about positive numbers, only first pair satisfies this requirement.
Solved.
===============
For your safety, Ignore writing by @josgarithmetic, since it leads you to "N O W H E R E".
Answer by TeachMath(96)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let larger number be N, which makes the smaller number: N - 6
Then N(N – 6) = N^2 + (N – 6)^2 – 223
Solve this to get: N, or larger number = 17
Smaller number: 17 – 6, or 11
That's all!!
|
|
|