Question 1110766: The price p and the quantity x sold of a certain product obey the demand equation below.
x equals negative 2 p plus 40 comma 0 less than or equals p less than or equals 20x=−2p+40, 0≤p≤20
(a)
Express the revenue R as a function of x.
(b)
What is the revenue if 44 units are sold?
(c)
What quantity x maximizes revenue? What is the maximum revenue?
(d)
What price should the company charge to maximize revenue?
(e)
What price should the company charge to earn at least $192 in revenue?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! i think that what you wanted to say is:
price p and quantity x obey the demand equation below:
x = -2p + 40, where 0 <= p <= 20
0 <= p <= 20
your revenue equation would be r = price * quantity = p * x.
r is the revenue
x is the number of units sold.
p is the price per unit.
the equation is r = p * x
you are given that x = -2p + 40
solve for p to get p = 20 - .5x
in the revenue equation of r = p * x, replace p with 20 - .5x to get:
r = (20 - .5x) * x
simplify to get r = 20x - .5x^2.
set the revenue equal to 0 and you get 0 = 20x - .5x^2
rearrange the terms to get this equation in standard quadratic form to get:
-.5x^2 + 20x = 0
in this form:
a = coefficient of x^2 term = -.5
b = coefficient of x term = 20
c = constant term = 0.
the maximum value of this quadratic equation is when x = -b/2a.
solve for x to get x = -20 / -1 = 20.
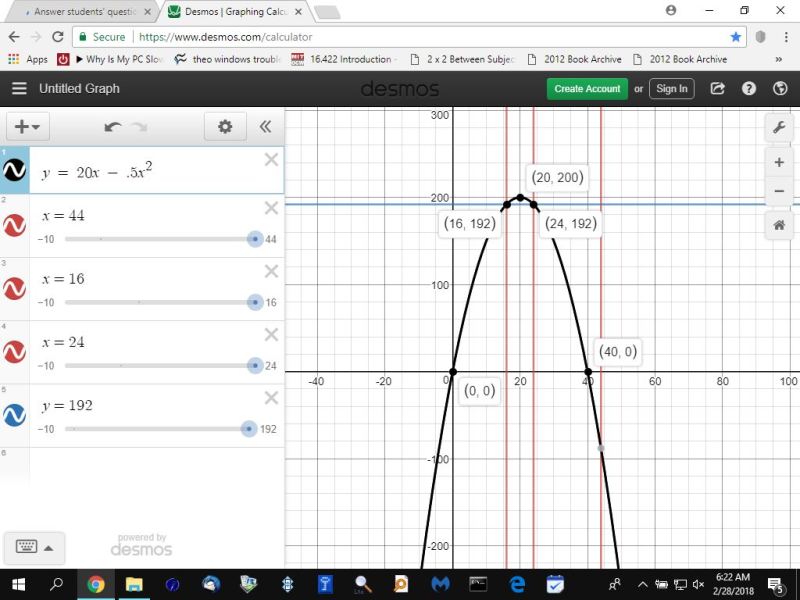
when x = 20, the original equation of r = 20x - .5x^2 becomes r = 20*20 - .5*20^2 which becomes r = 400 - 200 which results in r = 200.
your maximum revenue is 200 when x = 20
since r = x * p, then you can solve for p to get p - r/x, which becomes:
200/20 = 10
the price per shirt would have to be 10 in order to get a revenue of 200 when the quantity sold is 20.
20 * 10 = 200
you were previously given that x = -2p + 40
when x = 20, the equation becomes 20 = -2p + 40
subtract 40 from both sides to get -20 = -2p
divide both sides by -2 to get p = 10.
the price of 10 when the quantity sold is 20 confirms the solution that tells you that the maximum revenue is 200 when the quantity sold is 20.
answers to your questions are shown below:
(a)
Express the revenue R as a function of x.
r = 20x - .5x^2
(b)
What is the revenue if 44 units are sold?
when x = 44, r = 20x - .5x^2 becomes:
r = 20*44 - .5 * (44)^2 which becomes:
r = -88
since r = p * x, p would have had to be -2.
this solution is invalid, since your problem stated that 0 <= p <= 20.
therefore 44 units could not be sold, since, by the equation, x = 44 results in p = -2 which is out of the range of the permissible values of p.
if you go back to the original equation that says x = -2p + 40, then:
when p = 0, x = 40 and when p = 20, x = 0
therefore 0 <= p <= 20 translates to 0 <= x <= 40
x = 44 is out of the permissible range of of both p and x.
(c)
What quantity x maximizes revenue? What is the maximum revenue?
when x = 20, r = 200.
this is when the maximum revenue occurs.
(d)
What price should the company charge to maximize revenue?
they should charge 10 dollars per unit.
(e)
What price should the company charge to earn at least $192 in revenue?
your equation is r = 20x - .5x^2
if you want the revenue to be greater than 192, then r must be > 192.
this means that 20x - .5x^2 must be greater than 192.
your equation becomes an inequality that says 20x - .5x^2 > 192
if you subtract 192 from both side of this inequality, you get:
20x - .5x^2 - 192 > 0
to find the 0 points, set 20x - .5x^2 - 192 = 0 and solve for x.
you will get x = 16 or x = 24.
that's when 20x - .5x^2 - 192 = 0
since 20x - .5x^2 represents the revenue, then that's when the revenue - 192 = 0 which means that's when the revenue = 192, because, when you add 192 to both sides of 20x - .5x^2 - 192 = 0, you get 20x - .5x^2 = 192, which is the same as saying revenue = 192.
so when x = 16 or when x = 24, the revenue is equal to 192.
to find out what interval the revenue is greater than 192, then pick values less than 16, greater than 24, between 16 and 24.
you will find that the revenue is greater than 192 when the quantity of x is > 16 and < 24.
the graph of the original revenue equation shows that to be true.
here's the graph.
|
|
|