SOLUTION: in a quadratic equation, a student made a mistake in copying the coefficient of x^(2) and got the roots of 2 and 3. Another student made a mistake copying the constant term and got

0.  Let the original equation be   = 0.     (1)


1.  After the 1-st student incorrectly copied the coefficient at  ,  the equation took the form

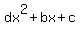     = 0.     (2)


    Since its roots are 2 and 3, we have this decomposition

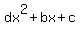     = d*(x-2)*(x-3),     or

     = .

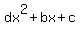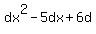    So, the original equation (1) has the two lowest degree terms -5dx + 6d:

         =     (3)

    with some unknown coefficients  "a"  and  "d".



2.   After the 2-nd student incorrectly copied the constant term,  the equation took the form

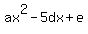     = 0.     (4)


    Since its roots are 4 and 6, we have this decomposition

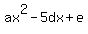     = a*(x-4)*(x-6),     or

     = .

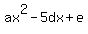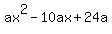    It implies  -5d = -10a,  which in turn  implies  d = 2a.

    Now from (3) we conclude that the original equation (polynomial) is/was

         = .

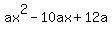    Its roots are the same as for equation 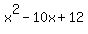  = 0.

    And they are   =  = .


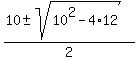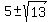Answer.  The roots of the original equation are   =   and   = .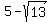