Question 1103806: according to the national association of rocketry the current model rocket altitude record in the f altitude events for ages 14 through 18 division is 1430 meters. from this record-setting altitude, the rocket is motionless as it begins his free fall the sat back to the ground using the equations, h (t)=-4.9t^2+v^0t+h^0find how long it will take here for the rocket to hit the ground after reaching its high point. (Hint: motionless implies and hitting the ground implies)
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
It to omit all the literature, or, better to say, if translate this literature to Math or Physics, it means the following:
How long it will take for freely falling body to hit the ground from the height of 1430 meters.
Using the equation h(t) = -4.9*t^2 + 0*t + 1430 (where "0" means the zero initial velocity, or motionless condition at the highest point
of the trajectory),
getting ground level means h(t) = 0, so you need to solve this quadratic equation
-4.9*t^2 + 0*t + 1430 = 0, or
4.9*t^2 = 1430 ====> t^2 = 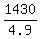 = 291.9 ====> t = = 291.9 ====> t = 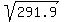 = 17.1 seconds (approximately).
Answer. 17.1 seconds (approximately). = 17.1 seconds (approximately).
Answer. 17.1 seconds (approximately).
|
|
|