Question 1087414: Find the standard form f(x)=a(x-h)^2+k of the quadratic function that has zeros of 1/5 and 9/5, and has it's vertex at the point (1,-1).
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39617)   (Show Source):
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website! Find the standard form f(x)=a(x-h)^2+k of the quadratic function that has zeros of 1/5 and 9/5, and has it's vertex at the point (1,-1).
Why don't you look at a similar problem you posted earlier, and try this one?
Don't you think that's a better way to learn how to do the problem, especially when you get it right?
Whatever you do, DO NOT follow the GARBAGE the other person suggested. Just substitute a point, preferably 
and the vertex, 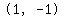 for (x, y) and (h, k), respectively, in the VERTEX form of a parabolic-equation, to get the value of "a."
Then substitute "a" and (h, k) to get the equation, in VERTEX form.
|
|
|
