SOLUTION: Here's a math problem that I have and do not know how to do at all: Suppose A and B are single digit positive integers chosen independently and at random. What is the probability

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: Here's a math problem that I have and do not know how to do at all: Suppose A and B are single digit positive integers chosen independently and at random. What is the probability       Log On


   

Question 1072012: Here's a math problem that I have and do not know how to do at all:
Suppose A and B are single digit positive integers chosen independently and at random. What is the probability that the point (a,b) lies above the parable y=ax^2-bx?
Answer by Fombitz(32388) About Me  (Show Source):
You can put this solution on YOUR website!
So when x=a,
y=a%28a%5E2%29-ba
y=a%5E3-ba
If y=b,
b=a%5E3-ba
b%2Bba=a%5E3
b%281%2Ba%29=a%5E3
b=a%5E3%2F%281%2Ba%29
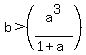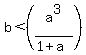So if b%3E%28a%5E3%2F%281%2Ba%29%29, then the point is above the curve and if b%3C%28a%5E3%2F%281%2Ba%29%29, then the point is below the curve.
So you can make a chart (I used EXCEL),
.
.
.
.
.
I cut it off because all remaining points show FALSE, (a,b) is below the curve.
So there are 81 possible outcomes, 19 of them have the point above the curve,
P=19%2F81
.
.
.
A couple of data points shown with their accompanying graphs,
.
.
.
.