Question 1068750: Without solving the given equation, find an equation whose roots are the squares of the roots of x^2 + 4x + 2 = 0.
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Without solving the given equation, find an equation whose roots are the squares of the roots of x^2 + 4x + 2 = 0.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The trick and the focus is to find the second equation without solving the first.
In this sense the solution by "josgarithmetic" is "out of the target".
I will show you how to strike EXACTLY to the target.
It is about the Vieta's theorem, whether it is included or not included to the school math curriculum.
Let "s" and "t" be the roots of the quadratic polynomial
p(x) = 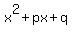 with the leading coefficient 1 at
with the leading coefficient 1 at  . Then the Vieta's theorem says:
s + t = -p and s*t = q.
For the given equation . Then the Vieta's theorem says:
s + t = -p and s*t = q.
For the given equation
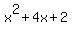 = =  it means that if "s" and "t" are its roots, then
s + t = -4, (1) and
s*t = 2. (2)
Next, if (1) and (2) are held, then
it means that if "s" and "t" are its roots, then
s + t = -4, (1) and
s*t = 2. (2)
Next, if (1) and (2) are held, then
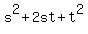 = = 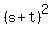 = =  = 16; hence, = 16; hence, 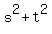 = 16 - 2s*t = 16 - 2*2 = 12, and = 16 - 2s*t = 16 - 2*2 = 12, and
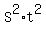 = = 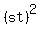 = = 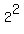 = 4.
Hence, by applying the Vieta;s theorem once again, you see that = 4.
Hence, by applying the Vieta;s theorem once again, you see that 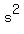 and and  are the roots of the polynomial
g(x) = are the roots of the polynomial
g(x) = 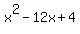 .
It is the answer to the problem's question. The problem is solved !!
Notice, we get the answer without solving the original equation.
Exactly as assigned by the condition.
All we did we manipulated with coefficients and used the Vieta's theorem.
On the way you learned about Vieta's theorem for quadratic equations and polynomials. .
It is the answer to the problem's question. The problem is solved !!
Notice, we get the answer without solving the original equation.
Exactly as assigned by the condition.
All we did we manipulated with coefficients and used the Vieta's theorem.
On the way you learned about Vieta's theorem for quadratic equations and polynomials.
Happy learning !!
|
|
|