.
Answer. 11 and 7.
Solution
 = 72 --->
(x-y)*(x+y) = 72.
But x-y = 4, according to the condition. Hence,
4*(x+y) = 72 --->
x + y =
= 72 --->
(x-y)*(x+y) = 72.
But x-y = 4, according to the condition. Hence,
4*(x+y) = 72 --->
x + y = 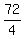 = 18.
So, you have two equations:
x + y = 18,
x - y = 4.
Add them.
From this point, please complete the solution on your own.
= 18.
So, you have two equations:
x + y = 18,
x - y = 4.
Add them.
From this point, please complete the solution on your own.