.
Find all real and complex zeros of the polynomial, and write p(x) as the product of linear factors.
P(x)=x^4-9x^2+4x+12
~~~~~~~~~~~~~~~~~~~~~~~~
Apply grouping to factor P(x):
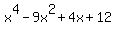 =
= 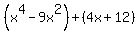 =
= 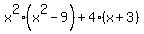 =
= 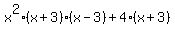 =
= 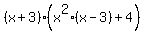 =
= 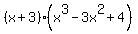 .
So, one root is x = -3.
Next, transform and factor the polynomial Q(x) = x^3 - 3x^2 + 4.
Add and distract x^2 and then apply grouping, again:
.
So, one root is x = -3.
Next, transform and factor the polynomial Q(x) = x^3 - 3x^2 + 4.
Add and distract x^2 and then apply grouping, again:
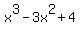 =
= 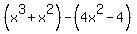 =
= 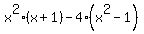 =
= 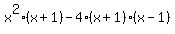 =
= 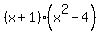 =
=  .
The roots of the polynomial Q(x) are -1, -2, 2.
Answer. The roots of the polynomial P(x) are -3, -2, -1, and 2.
.
The roots of the polynomial Q(x) are -1, -2, 2.
Answer. The roots of the polynomial P(x) are -3, -2, -1, and 2.