SOLUTION: Use the discriminant to determine whether the following equations have real solutions:0.0134x² + 0.0414 x + 0.0304 = 0

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: Use the discriminant to determine whether the following equations have real solutions:0.0134x² + 0.0414 x + 0.0304 = 0       Log On


   

Question 1047203: Use the discriminant to determine whether the following equations have real solutions:0.0134x² + 0.0414 x + 0.0304 = 0
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
An equation of the form ax%5E2%2Bbx%2Bc=0 ,
with real numbers a , b , and c ,
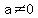where a%3C%3E0 is called a quadratic equation.
0.0134x%5E2+%2B+0.0414+x+%2B+0.0304+=+0 is a quadratic equation.
There is a formula to find the solutions to a quadratic equation, called the quadratic formula:
x+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+ .
The expression b%5E2-4%2Aa%2Ac that is under the square root is called the determinant.
The result of the quadratic formula is one or two real numbers if and only if
the determinant is not negative:
b%5E2-4%2Aa%2Ac%3E=0 .
(If b%5E2-4%2Aa%2Ac=0 there is only one solution; if b%5E2-4%2Aa%2Ac%3E0 there are two different real solutions).
In the case of the quadratic equation 0.0134x%5E2+%2B+0.0414+x+%2B+0.0304+=+0 ,
a=0.0134 ,
b=0.0414 , and
c=+0.0304+ , so
b%5E2-4%2Aa%2Ac+=+0.0414%5E2-4%2A0.0134%2A0.0304+=+0.00171396+-+0.0162944=0.00008452%3E0 ,
so there will be 2 real solutions.