You can
put this solution on YOUR website! .
The rate filled a tank with water is represented by the the equation r(t)=6t^2+3t-2 gallons per second.
how many gallons of water will be in the tank for the first 5 seconds?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Integral of r(t) from 0 (zero) to 5 seconds.
Which is V(t) = 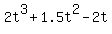 at t = 5.
Which is
at t = 5.
Which is  = 2*125 + 1.5*25 - 10 = 277.5 gallons.
= 2*125 + 1.5*25 - 10 = 277.5 gallons.