SOLUTION: If $s$ is a real number, then what is the smallest possible value of $2s^2 - 8s + 19$?

1.  Firmly memorize this:

    A quadratic function  y =   has a minimum/maximum at  x = 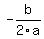.     (1)

    To find this maximum/minimum value, substitute  x = 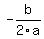  into the quadratic function. 
    Then min/max, after calculations, is 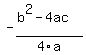 .                              (2)

    Next,  if  a > 0  then the parabola is open up and the min/max is the minimum.
           If  a < 0  then the parabola is open down and the min/max is the maximum.


2.  In your case,  the minimum is at s = 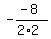 = 2.
    To calculate 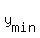, substitute s = 2 into the quadratic function.  It will produce the same value as (2), but the calculations are easier.

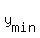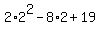     =  = 8 - 16 + 19 = 11.

Next, memorize this:


     It doesn't matter which letter of the English alphabet is used in the parabola equation as a variable. 
     To find a min/max and a vertex coordinates, always use the formula (1). It works ALWAYS.

     After finding x, calculate the value of a min/max by substituting the found value  of "x" into the parabola equation.