Question 1040183: Suppose that the roots of x^2+px+q=0 are rational numbers and p,q are integer, then show that the roots are integers.
Plzz help thanks in advance
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website!
x²+px+q = 0
The solutions are
 and and 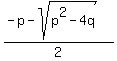 We know that the solutions are rational, so the
discriminant p²-4q is the square of an integer n,
then
p²-4q = n² and the solutions are
p²-n² = 4q
We know that the solutions are rational, so the
discriminant p²-4q is the square of an integer n,
then
p²-4q = n² and the solutions are
p²-n² = 4q 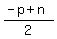 and and 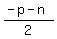 (p-n)(p+n) = 4q
1. The right side 4q is even so the left side (p-n)(p+n) is even.
2. The sum or difference of two even integers is even.
3. The sum or difference of two odd integers is even.
4. The sum or difference of an even and an odd integer is odd.
5. The product of two even integers is even.
6. The product of two odd integers is odd.
7. If an integer is odd, so is its opposite.
8. An even integer divided by 2 is an integer.
Case 1. p is even and n is odd
Then by 4, p-n and p+n are both odd.
Then by 6, (p-n)(p+n) is odd.
That contradicts 1. Thus case 1 is ruled out.
Case 2. p is odd and n is even
Then by 4, p-n and p+n are both odd.
Then by 6, (p-n)(p+n) is odd.
That contradicts 2. Thus case 2 is ruled out.
Case 3. p and n are both even
Then because of 2 and 7,
-p+n and -p-n are both even
Therefore, by 8,
(p-n)(p+n) = 4q
1. The right side 4q is even so the left side (p-n)(p+n) is even.
2. The sum or difference of two even integers is even.
3. The sum or difference of two odd integers is even.
4. The sum or difference of an even and an odd integer is odd.
5. The product of two even integers is even.
6. The product of two odd integers is odd.
7. If an integer is odd, so is its opposite.
8. An even integer divided by 2 is an integer.
Case 1. p is even and n is odd
Then by 4, p-n and p+n are both odd.
Then by 6, (p-n)(p+n) is odd.
That contradicts 1. Thus case 1 is ruled out.
Case 2. p is odd and n is even
Then by 4, p-n and p+n are both odd.
Then by 6, (p-n)(p+n) is odd.
That contradicts 2. Thus case 2 is ruled out.
Case 3. p and n are both even
Then because of 2 and 7,
-p+n and -p-n are both even
Therefore, by 8, 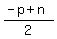 and and 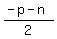 are both
integers. The proof is complete for case 3.
Case 4. p and n are both odd
Then because of 3 and 7
-p+n and -p-n are both even
Therefore, by 8, are both
integers. The proof is complete for case 3.
Case 4. p and n are both odd
Then because of 3 and 7
-p+n and -p-n are both even
Therefore, by 8, 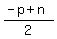 and and 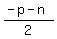 are both
integers. The proof is complete for case 4.
Edwin are both
integers. The proof is complete for case 4.
Edwin
|
|
|