SOLUTION: Hailey is riding a hot-air balloon and accidentally drops her purse over the side. The table shows the height of her purse at different times. When will her purse reach the ground?

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: Hailey is riding a hot-air balloon and accidentally drops her purse over the side. The table shows the height of her purse at different times. When will her purse reach the ground?      Log On


   

Question 1032514: Hailey is riding a hot-air balloon and accidentally drops her purse over the side. The table shows the height of her purse at different times. When will her purse reach the ground? Show calculations.
Time (s) - 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Height (m) - 1000, 995, 980, 955, 920, 875, 820, 755, 680, 595, 500
Thanks
Answer by robertb(5830) About Me  (Show Source):
You can put this solution on YOUR website!
The values for the heights are given recursively as
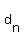a%5Bn%2B1%5D+=+a%5Bn%5D+%2B+d%5Bn%5D, where d%5Bn%5D is an AP with a%5B1%5D+=+-5 and common difference d = -10. Indeed,
d%5Bn%5D+=+-5+%2B+%28n-1%29%28-10%29+=+5+-+10n. Now
a%5B2%5D+=+a%5B1%5D+%2B+d%5B1%5D,
a%5B3%5D+=+a%5B2%5D+%2B+d%5B2%5D,
a%5B4%5D+=+a%5B3%5D+%2B+d%5B3%5D,
.........................
a%5Bn-1%5D+=+a%5Bn-2%5D+%2B+d%5Bn-2%5D,
a%5Bn%5D+=+a%5Bn-1%5D+%2B+d%5Bn-1%5D,
a%5Bn%2B1%5D+=+a%5Bn%5D+%2B+d%5Bn%5D,
Adding all the corresponding sides of these equations gives
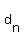a%5Bn%2B1%5D+=+a%5B1%5D+%2Bd%5B1%5D+%2B+d%5B2%5D+...+ d%5Bn%5D.
<==> a%5Bn%2B1%5D+=+a%5B1%5D%2B+%28n%2F2%29%28-5+%2B+5-10n%29+=+1000+-+5n%5E2, for n%3E=0.
==> a%5Bn%5D+=+1000+-+5%28n-1%29%5E2.
Hence let a%5Bn%5D+=+1000+-+5%28n-1%29%5E2+=+0.
==> n+=+1%2B+10sqrt%282%29+=+15.14 seconds, the time her purse reaches the ground.