Question 1030562: For each quadratic function, state the vertex and then graph the function
Julie wants to place 44 ft of picket fencing around a garden so as to create the largest rectangular area possible.
A.) If x represents the width, write an algebraic expression that represents the length
B.) Write a function rule, f(x), that models the area of the garden
C.) What is the minimum point on the parabola?
D.) Find the dimensions of the garden with the maximum area
E.) What is the maximum area?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! ): For each quadratic function, state the vertex and then graph the function
Julie wants to place 44 ft of picket fencing around a garden so as to create the largest rectangular area possible.
A.) If x represents the width, write an algebraic expression that represents the length
The perimeter of the garden is 44 ft, therefore:
2L + 2x = 44
simplify, divide by 2
L + x = 22
L = -x+22, represents the length
:
B.) Write a function rule, f(x), that models the area of the garden
f(x) = x(-x+22)
f(x) = -x^2 + 22x
:
C.) What is the maximum point on the parabola? (Only maximum would make sense)
the maximum point occurs on the axis of symmetry x = b/(2a)
x = 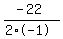
x = 11 ft is the x value for the max point
:
D.) Find the dimensions of the garden with the maximum area
L = -11 + 22
L = 11 ft, obviously, it is a square
:
E.) What is the maximum area?
11^2 = 121 sq/ft
|
|
|