SOLUTION: A diver jumps off a diving board that is 10 ft above the water at a velocity of 12 ft/sec. His height, s , in feet, above the water can be modeled by {{{s(t)=-16t^2+12t+10}}}

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: A diver jumps off a diving board that is 10 ft above the water at a velocity of 12 ft/sec. His height, s , in feet, above the water can be modeled by {{{s(t)=-16t^2+12t+10}}}       Log On


   

Question 1030179: A diver jumps off a diving board that is 10 ft above the water at a velocity of 12 ft/sec. His height, s , in feet, above the water can be modeled by
s%28t%29=-16t%5E2%2B12t%2B10

(a) How long is the diver in the air before he hits the water?
Enter the exact answer.
The diver is in the air for ____ seconds.
(b) What is the maximum height achieved and when does it occur?
Enter the exact answers.
The maximum height is ____ feet, and it occurs after ____seconds.
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
The diver's height, s (in feet), above the water can be modeled by
s%28t%29=-16t%5E2%2B12t%2B10 for 0%3C=t%3CT ,
where t is the time since the diver jumped off the diving board, and
T is the total time (in seconds) that the diver is in the air.
Negative times make no sense, because the model equation/function cannot predict how high above the water the diver was at various times before jumping off the board.
Times after the diver hits the water make no sense either. The model will not work for those times.

(a) The diver hits the water at t=T, when the diver's height, s (in feet), above the water is
s%28T%29=0 , so
-16T%5E2%2B12T%2B10=0
To solve that quadratic equation we could
use the quadratic formula, or
factor the quadratic polynomial, or
"complete the square".
FACTORING:
We notice that -16%2A10=-160 can be factored many ways,
but one of them, 20%29%28-8%29=-160 , has factors that add to the middle coefficient:
20-8=12 .
So we re-write the polynomial (and the equation) as
-16T%5E2-8T%2B20T%2B10=0 , and factor by parts:
-16T%5E2-8T%2B20T%2B10=0-->-8T%282T%2B1%29%2B20%282T%2B1%29=0-->%28-8T%2B10%29%282T%2B1%29=0 .
The solutions to that equation,
coming from system%282T%2B1=0%2C%22or%22%2C-8T%2B10=0%29
are T=-1%2F2 and T=10%2F8=1.25 .
Since the function was defined for a domain of 0%3C=t%3C=T ,
the only solution that makes sense is highlight%28T=1.25%29 .
The diver is in the air for highlight%281.25%29 seconds.
COMPLETING THE SQUARE:
-16T%5E2%2B12T%2B10=0-->16T%5E2-12T=10-->%284T%29%5E2-12T=10-->%284T%29%5E2-2%284T%29%283%2F2%29%2B%283%2F2%29%5E2=10%2B%283%2F2%29%5E2-->%284T-3%2F2%29%5E2=10%2B9%2F4-->%284T-3%2F2%29%5E2=49%2F4 .
So, either 4T-3%2F2=-sqrt%2849%2F4%29=-7%2F2%29 or 4T-3%2F2=sqrt%2849%2F4%29=7%2F2%29 .
4T-3%2F2=7%2F2%29-->4T=7%2F2%2B3%2F2-->4T=10%2F2-->T=10%2F8=highlight%281.25%29 .
The other choice, 4T-3%2F2=-7%2F2%29 , yields a negative value for T ,
which is not in the domain where the model function should be defined,
and it would not make sense to say that the diver is in the air for a negative number of seconds after jumping off the board.

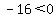(b) s%28t%29=-16t%5E2%2B12t%2B10 is a quadratic function with the negative leading coefficient -16%3C0 .
APPLYING FORMULAS:
A formula that your teacher may have wanted to make you memorize says that a quadratic function
f%28x%29=ax%5E2%2Bbx%2Bc with a negative leading coefficient, a%3C0 ,
has a maximum for x=%28-b%29%2F%222+a%22 .
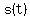In this case, we have t instead of x , and s%28t%29 instead of f%28x%29 .
Then, we have a=-16%3C0 , and b=12 .
So, the maximum height happens at t=%28-12%29%2F%282%2A%28-16%29%29=12%2F32=3%2F8=highlight%280.375%29 .
At that time, the height is
.
JUST USING YOUR AWESOME KNOWLEDGE OF BASIC ALGEBRA, BECAUSE YOU'D RATHER REASON THAN MEMORIZE AND APPLY FORMULAS:
s%28t%29=-16t%5E2%2B12t%2B10
s%28t%29=-16%28t%5E2-%283%2F4%29t%29%2B10
s%28t%29=-16%28t%5E2-%283%2F4%29t%2B%283%2F8%29%5E2-%283%2F8%29%5E2%29%2B10
s%28t%29=-16%28t%5E2-%283%2F4%29t%2B%283%2F8%29%5E2-9%2F64%29%2B10
s%28t%29=-16%28%28t-3%2F8%29%5E2-9%2F64%29%2B10
s%28t%29=-16%28t-3%2F8%29%5E2-%289%2F64%29%28-16%29%2B10
s%28t%29=-16%28t-3%2F8%29%5E2%2B9%2F4%2B10
s%28t%29=-16%28t-3%2F8%29%5E2%2B49%2F4
Since %28t-3%2F8%29%5E2%3E=0 , s%28t%29=-16%28t-3%2F8%29%5E2%2B49%2F4%3C=49%2F4=highlight%2812.25%29 ,
and s%28t%29=12.25 only when t-3%2F8=0<-->t=3%2F8=highlight%280.375%29 .

Either way you can get to the answer,
the maximum height is highlight%2812.25%29 feet, and it occurs after highlight%280.375%29 seconds.