Question 1026782: If s is a real number, then what is the smallest possible value of 2s^2 - 8s + 19?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  is a quadratic polynomial. is a quadratic polynomial.
Quadratic functions such as  with {{a<>0}}} , with {{a<>0}}} ,
have a maximum (if  ), ),
or a minimum (if  ). ).
So, since the coefficient of 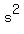 is is 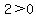 , ,
 has a minimum value}}} . has a minimum value}}} .
How could you find that minimum value?
You could remember and apply a recipe handed down by your algebra 2 teacher.
Alternatively, you could use your knowledge of algebra, and your ability to think.
APPLYING MEMORIZED FORMULAS/RECIPES:
A quadratic function {{f(x)=ax^2+bx+c}}} with  has a minimum for has a minimum for  . .
In the case of  , ,
the variable is  rather than rather than  , ,  and and  , ,
so the minimum happens for  , ,
and for  , ,  . .
IF YOU DID NOT MEMORIZE THAT FORMULA,
you have to reason your way to the answer.
 may remind you of may remind you of  , ,
and  . .
So, you can complete the square:
 . .
You know that the square of any real number is non-negative,
so  , and , and  , ,
which means the the smallest possible value of  is is  . .
|
|
|