You can
put this solution on YOUR website! .
For what value of the constant k does the quadratic 2x^2 - 5x + k= 0 have a double root?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Calculate the discriminant d =  = (-5)^2 - 4*2*k = 25 - 8k.
The double root will happen when the discriminant is zero: d = 0.
It gives k =
= (-5)^2 - 4*2*k = 25 - 8k.
The double root will happen when the discriminant is zero: d = 0.
It gives k = 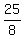 .
.