SOLUTION: I need help with this problem. Please help me and show all work. Thanks A person standing close to the edge on top of a 144-foot building throws a ball vertically upward. The

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: I need help with this problem. Please help me and show all work. Thanks A person standing close to the edge on top of a 144-foot building throws a ball vertically upward. The       Log On


   

Question 1021026: I need help with this problem. Please help me and show all work. Thanks

A person standing close to the edge on top of a 144-foot building throws a ball vertically upward. The quadratic function h(t)=−16t^2+128t+144
h(t)=-16t^2+128t+144 models the ball's height about the ground, h(t)
in feet, t seconds after it was thrown.
a) What is the maximum height of the ball?
_________feet
b) How many seconds does it take until the ball hits the ground?
_________ seconds
Found 2 solutions by KMST, MathTherapy:
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
WITHOUT ALGEBRA 2:
h%28t%29=-16t%5E2%2B128t%2B144
h%28t%29=-16%28t%5E2%2B128t%2F%28-16%29%2B144%2F%28-16%29%29
h%28t%29=-16%28t%5E2-8t-9%29
h%28t%29=-16%28t%5E2-8t%2B16-16-9%29
h%28t%29=-16%28%28t%5E2-8t%2B16%29-25%29
h%28t%29=-16%28%28t-4%29%5E2-25%29
h%28t%29=-16%28t-4%29%5E2-16%2A%28-25%29
h%28t%29=-16%28t-4%29%5E2%2B400

a) From the last equation above we realize that
h%28t%29%3C=400 ,
so the maximum height of the ball is highlight%28400%29 feet.

b) The ball hits the ground when 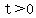h%28t%29=-16t%5E2%2B128t%2B144=0 for a t%3E0 ,
so we need a positive solution for -16%28%28t-4%29%5E2-25%29=0 .
-16%28%28t-4%29%5E2-25%29=0<-->%28t-4%29%5E2-25=0<-->%28t-4%29%5E2=25-->system%28t-4=5%2C%22or%22%2Ct-4=-5%29 .
t-4=5<-->t=4%2B5-->t=9 is the only option with t%3E0 ,
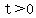so the ball hits the ground highlight%289%29 seconds after it is thrown upwards.
WITH FORMULAS:
a) A quadratic function f%28x%29=ax%5E2%2Bbx%2Bc with x%3C0
has a maximum for x=%28-b%29%2F%282%2Aa%29 .

h%28t%29=-16t%5E2%2B128t%2B144 is such a function with x=t , a=-16%3C0, and b=128 ,
so there is a maximum for
t=%28-128%29%2F%282%2A%28-16%29%29=%28-128%29%2F%28-32%29=4 , and that maximum is
.

b) The ball hits the ground when 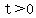h%28t%29=-16t%5E2%2B128t%2B144=0 for a t%3E0 .
So, we are looking for a positive solution to
-16t%5E2%2B128t%2B144=0<-->16t%5E2-128t-144=0<-->16t%5E2%2F16-128t%2F16-144%2F16=0<-->t%5E2-8t-9=0 .

Since the solutions are t=9 and t=-1 ,
the ball hits the ground highlight%289%29 seconds after it is thrown upwards.

The equation t%5E2-8t-9=0 can be solved by factoring, by "completing the square", and by using the quadratic formula.
By factoring:
t%5E2-8t-9=0
%28t%2B1%29%28t-9%29=0--->system%28t%2B1=0%2C%22or%22%2Ct-9=0%29--->system%28t=-1%2C%22or%22%2Ct=9%29
By using the quadratic formula:
The quadratic formula says that any solution(s) for
ax%5E2%2Bbx%2Bc=0 , if there is any, are given by
x+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+ ,
so any solution(s) for t%5E2-8t-9=0 ,
with system%28t=x%2Ca=1%2Cb=-8%2Cc=-1%29 , would be given by
-->system%28t=%288%2B10%29%2F2=18%2F2=9%2C%22or%22%2Ct=%288-10%29%2F2=%28-2%29%2F2=-1%29 .
Completing the square is pretty much what was done at the top:
t%5E2-8t-9=0t%5E2-8t-9=0<-->t%5E2-8t%2B16=9%2B16<-->%28t-4%29%5E2=25-->system%28t-4=5%2C%22or%22%2Ct-4=-5%29-->system%28t=5%2B4=9%2C%22or%22%2Ct=-5%2B4=-1%29

Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!

I need help with this problem. Please help me and show all work. Thanks

A person standing close to the edge on top of a 144-foot building throws a ball vertically upward. The quadratic function h(t)=−16t^2+128t+144
h(t)=-16t^2+128t+144 models the ball's height about the ground, h(t)
in feet, t seconds after it was thrown.
a) What is the maximum height of the ball?
_________feet

b) How many seconds does it take until the ball hits the ground?
_________ seconds
Maximum height occurs at x+=+%28-+b%29%2F%282a%29, or at x+=+%28-+128%29%2F%282+%2A+-+16%29, or at: x+=+4

Maximum height at x+=+4 is: y+=+-+16%284%29%5E2+%2B+128%284%29+%2B+144, or y+=+-+256+%2B+512+%2B+144, or maximum height reached = highlight_green%28matrix%281%2C2%2C+400%2C+ft%29%29 



Ball hits the ground when y, or height = 0, so we get:

0+=+-+16t%5E2+%2B+128t+%2B+144

-+16%280%29+=+-+16%28t%5E2+-+8t+-+9%29 ---- Factoring out GCF, - 16

0+=+t%5E2+-+8t+-+9  

0 = (t - 9)(t + 1)

0 = t - 9        OR          0 = t + 1

t, or time it takes ball to hit the ground = highlight_green%28matrix%281%2C2%2C+9%2C+seconds%29%29            OR          - 1 = t (ignore)