Question 1011284: If r and s are the roots of x^2 -8x +6 =0, find r^2 + 3rs +s^2. Thank you.
Found 3 solutions by solver91311, ikleyn, MathTherapy:
Answer by solver91311(24713)   (Show Source): (Show Source):
Answer by ikleyn(52781)   (Show Source): (Show Source):
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! If r and s are the roots of x^2 -8x +6 =0, find r^2 + 3rs +s^2. Thank you.
Sum of roots: 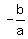 , or , or 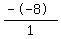 , or 8 , or 8
Product of roots:  , or , or  , or 6 , or 6
Therefore, r + s = 8, and rs = 6
 , but , but  , so , so  , or 64 + 6, or , or 64 + 6, or 
|
|
|