SOLUTION: Solve the exercise by solving a system of equations. Find the quadratic equation of the form y = ax^2 + bx + c whose graph passes through the points(2, 4),(-2, 8),and (1,-4).

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: Solve the exercise by solving a system of equations. Find the quadratic equation of the form y = ax^2 + bx + c whose graph passes through the points(2, 4),(-2, 8),and (1,-4).       Log On


   

Question 1008243: Solve the exercise by solving a system of equations.
Find the quadratic equation of the form y = ax^2 + bx + c
whose graph passes through the points(2, 4),(-2, 8),and (1,-4).



Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
You want to find the equation of this parabola. Scroll down:



(2, 4),(-2, 8),and (1, -4)

y%22%22=%22%22ax%5E2%2Bbx%2Bc

For the point (2, 4), substitute x = 2 and y = 4

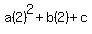4%22%22=%22%22a%282%29%5E2%2Bb%282%29%2Bc

For the point (-2, 8), substitute x = -2 and y = 8

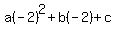8%22%22=%22%22a%28-2%29%5E2%2Bb%28-2%29%2Bc

For the point (1, -4), substitute x = 1 and y = -4

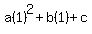-4%22%22=%22%22a%281%29%5E2%2Bb%281%29%2Bc

That gives us the system of three equations in three
unknowns a,b, and c



Simplify those equations:



system%284=4a%2B2b%2Bc%2C8=4a-2b%2Bc%2C-4=a%2Bb%2Bc%29

Swap the sides of the equations so the system will look "normal":

system%284a%2B2b%2Bc=4%2C4a-2b%2Bc=8%2Ca%2Bb%2Bc=-4%29

Solve that by elimination.  Then substitute the values you get
for a, b, and c in 

y%22%22=%22%22ax%5E2%2Bbx%2Bc

If you run into any trouble finishing, ask me in the thank-you note 
form below, and I'll get back to you by email.  

Edwin