Question 1003127: Given a>0 for what values of k does y=a(x-k)^2+k have?
a) two x-intercepts ?
b) one x intercept ?
c) no x-intercepts?
Please explain why for each one. Thank you.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The x-intercepts, if any, are the points where  (or the values of (or the values of  for those points). for those points).
IF YOU WERE NOT TAUGHT ABOUT THE DISCRIMINANT OF A QUADRATIC EQUATION:
The x-intercepts, if any, are the points where  (or the values of (or the values of  for those points). for those points).
For  the function is the function is  , and has one x-intercept at , and has one x-intercept at 
For  , since , since  for all values of for all values of  , ,
 , meaning that there is no x-intercept. , meaning that there is no x-intercept.
For  , there are two intercepts, because , there are two intercepts, because 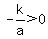 , so , so 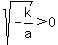 , and , and
 --> --> --> --> --> --> --> --> --> --> . .
IF YOU WERE TAUGHT ABOUT THE DISCRIMINANT OF A QUADRATIC EQUATION:
The reasoning above is still valid, but you may be expected to talk about the discriminant in an answer.
That makes it complicated, but here it goes:
 <---> <---> <---> <---> <---> <--->
For a quadratic equation of the form  , ,
 . .
If  , ,  has two solutions; has two solutions;
if  , ,  has one solution, and has one solution, and
if  , ,  has no solution. has no solution.
Applied to  , ,
where  and and  , ,
 , so , so
if 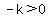 <--> <--> , ,  has two solutions, and has two solutions, and  has two x-intercepts; has two x-intercepts;
if  <--> <--> , ,  has one solutions, and has one solutions, and  has one x-intercepts, and has one x-intercepts, and
if  <--> <--> , ,  has no solutions, and has no solutions, and  has no x-intercepts. has no x-intercepts.
|
|
|