SOLUTION: The sum of the lengths of the two perpendicular sides of a right triangle is 30 centimeters. What are their lengths if the square of the hypotenuse is a minimum?

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: The sum of the lengths of the two perpendicular sides of a right triangle is 30 centimeters. What are their lengths if the square of the hypotenuse is a minimum?      Log On


   

Question 1002047: The sum of the lengths of the two perpendicular sides of a right triangle is 30 centimeters. What are their lengths if the square of the hypotenuse is a minimum?
Found 3 solutions by addingup, josgarithmetic, MathTherapy:
Answer by addingup(3677) About Me  (Show Source):
You can put this solution on YOUR website!
if the square of the hypotenuse is a minimum of what??

Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
h, hypotenuse
x and 30-x are lengths of the legs.
h%5E2=x%5E2%2B%2830-x%29%5E2
h%5E2=x%5E2%2B30%5E2-60x%2Bx%5E2
h%5E2=2x%5E2-60x%2B900

Find the x value or values for the minimum h%5E2.
2x%5E2-60x%2B900=0
x%5E2-30x%2B450=0
-
Discriminant, 900-4%2A450=NegativeNumber
This method, finding the roots, will not work here because h%5E2 as a function does not intersect the x-axis.

You can complete the square for making into standard form, and then read the vertex (a minimum point) from that form of the equation. The term to use is %2830%2F2%29%5E2=15%5E2, or 225.

x%5E2-30x%2B15%5E2%2B450-225=0
%28x-15%29%5E2%2B225=0
Showing x=15 for the vertex, and then one leg of the triangle is 15, and therefore the other leg is 30-x=30-15=15 also.

Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!
The sum of the lengths of the two perpendicular sides of a right triangle is 30 centimeters. What are their lengths if the square of the hypotenuse is a minimum?
The square of the hypotenuse is the sum of the squares of the legs

Therefore, their sum is 30, and the hypotenuse (SUM OF THEIR SQUARES) is a minimum (you may recall that: a%5E2+%2B+b%5E2+=+c%5E2)



Let longer leg be x, and shorter, y

Then we have: x + y = 30______y = - x + 30 ------- eq (i)

Also, y+=+x%5E2+%2B+y%5E2 -------- eq (ii)

y+=+x%5E2+%2B+%28-+x+%2B+30%29%5E2 ------- Substituting - x + 30 for y in eq (ii)

y+=+x%5E2+%2B+x%5E2+-+60x+%2B+900+

y+=+2x%5E2+-+60x+%2B+900



MINIMUM occurs at: x = 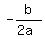-+b%2F%282a%29, or at: x+=+-+-+60%2F%282+%2A+2%29, or at x+=+60%2F4, or at: x = 15

With MINIMUM occurring at x = 15, we get: 

y = - 15 + 30 ----------- Substituting 15 for x in eq (i)

y = 15

Thus, length of each leg is: highlight_green%2815%29 cm