Question 993886: Hi
I am given this equation, h= height (meters), t= time (seconds)
h=2t(50-t)
How long is the rocket in air?
-I just applied the null factor law for that equation, and got:
2t = 0
t=0
and
50-t=0
-t=-50
t=50
Does that mean the rocket was in the air for 50 seconds?
or did i do something wrong or did not take in to account
thank you
Found 2 solutions by Alan3354, Theo:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! I am given this equation, h= height (meters), t= time (seconds)
h=2t(50-t)
How long is the rocket in air?
-I just applied the null factor law for that equation, and got:
2t = 0
t=0
and
50-t=0
-t=-50
t=50
Does that mean the rocket was in the air for 50 seconds?
or did i do something wrong or did not take in to account
===========================
No, you got it right.
It's launched at t = 0 and impacts at t = 50.
=========================
PS This is not a rocket. Rockets have thrust engines and accelerate upward. This is just a projectile.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! it appears the rocket was in the air for 50 seconds.
your equation was h = 2t * (50 - t)
this is a quadratic equation.
when you set it equal to 0, you find the x-intercepts.
those occur at t = 0 and t = 50.
since the coefficient of the leading term is negative, the quadratic equation points up and opens down.
to see this easier, simplify the equation by multiplying the factors out.
2t * (50 - t) = 100t - t^2
reorder the terms to get h = -t^2 + 100t
the leading coefficient is negative which makes the parabola (graph of a quadratic equation is a parabola) point up (maximum point is on top) and open down.
since all value of t have the graph positive between 0 and 50, that's the time that the graph of the equation is above the x-axis which represents the time the rocket is in the air.
here's what the graph of your equation looks like:
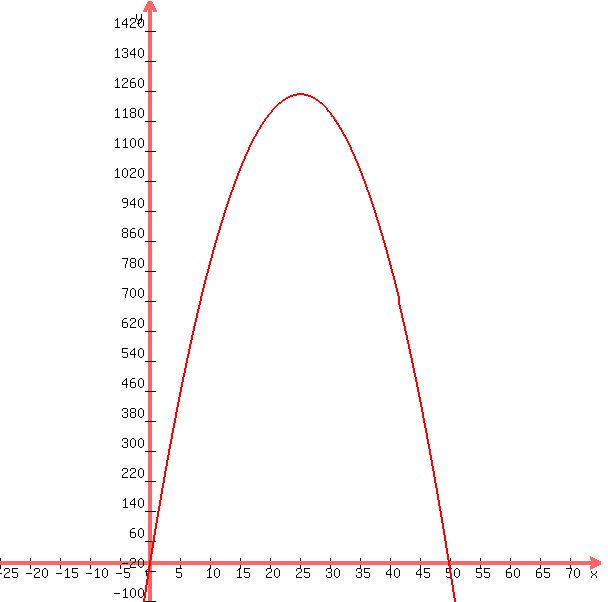
i used x instead of t because that's what the graphing software requires.
|
|
|