Question 992634: Find the minimum value of x^2-2x-8, if it has one.
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Does the graph of: have a maximumum and minimum? have a maximumum and minimum?
Well, it may have a maximum or it may have a minimum, but it doesn't have both!
The graph of a quadratic equation ( ), such as this, is called a "parabola" and a parabola has a maximum or a minimum depending upon whether it opens upwards (has a minimum) or opens downwards (has a maximum). ), such as this, is called a "parabola" and a parabola has a maximum or a minimum depending upon whether it opens upwards (has a minimum) or opens downwards (has a maximum).
You can tell which way the parabola opens by inspecting the coefficient of the  term, which is +1 in your problem. term, which is +1 in your problem.
If this coefficient is positive, then the parabola opens upwards and the graph has a minimum.
If the coefficient is negative,then the parabola opens downwards and the graph has a maximum.
The maximum/minimum point (also known as the "vertex") can be found as follows:
The x-coordinate of this point is:
 The a is the coefficient of the The a is the coefficient of the  term and the b is the coefficient of the term and the b is the coefficient of the  term. term.
In your equation,  and and  , so , so


 This is the x-coordinate of the vertex. This is the x-coordinate of the vertex.
To find the y-coordinate, substitute  into the given quadratic equation and solve for into the given quadratic equation and solve for  : :
 Substitute Substitute  . .



The vertex (or the 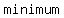 in this case) is at ( in this case) is at ( , ,  ) )
Let's see what the graph looks like:

|
|
|