Question 970776: Write a quadratic function in standard form whose graph passes through the given points. Use STAT
(1,2), (3,4), (6, -8)
Find the maximum heights.
What is the approximate difference in the maximum height for the parabolas?
Found 2 solutions by jim_thompson5910, Boreal:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! If you are using a calculator such as a TI83,TI84,etc, then
Step 1) Hit the STAT key and go to "edit". You'll see lists L1,L2,L3...
Step 2) Type the x coordinates of each point into list L1. So you are typing in 1,3,6 into list L1. The first column.
Step 3) Type the y coordinates of each point into list L2. So you are typing in 2,4,-8 into list L2. The second column.
Step 4) Hit the STAT key and scroll to the right once to get to the "Calc" menu. Then scroll down to "QuadReg". That stands for "Quadratic Regression". Hit enter twice to have the calculator compute the three coefficients a,b,c
Step 5) The calculator will report: a = -1, b = 5, c = -2
Any quadratic is in the form 
So the quadratic that goes through the three points (1,2), (3,4), (6, -8) is 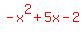
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! Using the calculator,
a=-1
b=5
c=-2
-x^2+5x-2=Y(x)
The maximum height is about at (2.5, 4,1)
The question asks for the approximate difference in the maximum heights for the parabola. The first sentence implies singular; the second one plural. I am just using quadratic regression.
Of note is the x=value is at -b/2a, which is 5/2 for x. The y-value would be 3 given this x.
If there were another part of this problem, please let me know. There are many parabolas that go through one of these points, but this is the best fit for the three points mentioned.

|
|
|