SOLUTION: Q1 (i) Factor the expression 4y^2-12xy-8yz+9x^2+12xz+4z^2 (ii) Expand the expression(3x-2y+3z)^3/(5x-2y+z)^2 (iii)

Here are the 1st and 3rd.
I haven't figured out the 2nd one yet.  
Is that the way it was given?  No errors?
Is it supposed to be a division?
You were asked to "expand a quotient"?  
That doesn't seem right.

Anyway here are the first and third ones:

Q1 (i) Factor the expression                          

                              

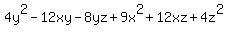Rearrange the terms as

 +  + 

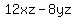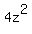The first three terms factor as  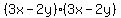or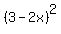 

We can take  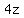out of the 
3rd and 4th terms and we now have



Now let 

Then the above becomes



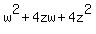which factors as

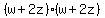 or



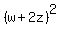Now replace the w by (3x-2y)



----------------------------------

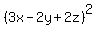(iii) Solve the equation:
      
 

We notice that the coefficients of the
1st, 3rd, and 5th terms are 1,1,-2, and that
the coefficients of the 2nd, 4th, and 6th
terms are -2,-2,4 and that these are
proportional, so we rearrange the terms:



Factor x out of the first 3 terms and -2
out of the last 3 terms:

 

Now we can take out the common factor 
 and we have:



Now we can factor the first parenthetical 
expression:



and finally factor the expression in 
the middle parentheses as the difference 
of two squares:



Now we set each factor = 0:

Setting first factor = 0




Use the principle of square roots  

    x = ±
    x = ±

Setting second factor = 0
    x - 1 = 0 gives x = 1

Setting third factor = 0
    x + 1 = 0 gives x = -1

Setting fourth factor = 0
    x - 2 = 0 gives x = 2

So the 5 solutions are ±i,1,-1, and 2  

Edwin