Question 821566: A rocket fired vertically upwards follows the law y=48t-8t^2
Plot a graph y against t for values of t from 0 to 6 seconds
By solving the quadratic equation  find the times t1 and t2 when the rocker is at a height of 'a' metres above the launch point.
Value of a is 25
Give final answer correct to 3 decimal places and check the answers using your graph.
Found 2 solutions by stanbon, TimothyLamb:
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website! A rocket fired vertically upwards follows the law y = 48t-8t2
Plot a graph y against t for values of t from 0 to 6 seconds
------------------------------
By solving the quadratic equation 8t^2-48t+a = 0 find the times
t1 and t2 when the rocker is at a height of 'a' metres above
the launch point.
Value of a is 25
t = [48+-sqrt(48^2-4*8*25)]/16 = [48+-38.78]/16
t1 = 0.5762
t2 = 5.4238
------------------------
Give final answer correct to 3 decimal places and
check the answers using your graph.
Cheers,
Stan H.
================
Answer by TimothyLamb(4379)  (Show Source):
You can put this solution on YOUR website! ---
the equation of projectile motion is given as:
h(t) = -8t^2 + 48t
---
at a= 25 meters:
---
h(t) = -8t^2 + 48t = 25
-8t^2 + 48t - 25 = 0
---
the above quadratic equation is in standard form, with a=-8, b=48, and c=-25
---
to solve the quadratic equation, by using the quadratic formula, copy and paste this:
-8 48 -25
into this solver: https://sooeet.com/math/quadratic-equation-solver.php
---
the two real roots (i.e. the two x-intercepts), of the quadratic are:
t = 0.576160071
t = 5.42383993
---
answer:
the rocket is at 25 meters height twice, at the following times in seconds after launch:
t = 0.576160071
t = 5.42383993
---
graph:
---
---
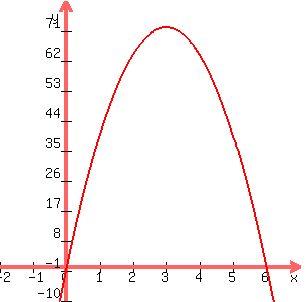
Solve and graph linear equations:
https://sooeet.com/math/linear-equation-solver.php
---
Solve quadratic equations, quadratic formula:
https://sooeet.com/math/quadratic-formula-solver.php
---
Solve systems of linear equations up to 6-equations 6-variables:
https://sooeet.com/math/system-of-linear-equations-solver.php
|
|
|
