Question 686537: whats the solution to x^2 +4x+19=0?
Found 2 solutions by jim_thompson5910, josh_jordan:
Answer by jim_thompson5910(35256)   (Show Source):
Answer by josh_jordan(263)  (Show Source):
You can put this solution on YOUR website! To solve the equation  , we can use the quadratic formula. We cannot use factoring because no two factors of 19 can be multiplied together to give us 19 and added together to give us 4. So, let's proceed with the quadratic formula:
In our original equation, a=1, b=4, and c=19. So, we will substitute each number for it's corresponding letter in our quadratic formula:
which breaks down to:
 =
Now, we have to reduce  :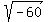
Factors of 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
Which of the factors is a perfect square? 4, because 2 x 2 = 4. And what number multiplied by 4, gives us 60? 15. So, 4 x 15 = 60
Remember that  , where i represents an imaginary number.
Now we can remove both the perfect square (4), and the -, which gives us:
We can factor out a 2 from our numerator, to give us:
Now, we can reduce the fraction, which gives us our final answer:
|
|
|
