Question 66052: In most businesses, increasing prices of products can negatively impact the number of customers. A bus company in a small town has an average number of riders of 800 per day. The bus company charges $2.25 for a ride. They conducted a survey of their customers and found that they will lose approximately 40 customers per day for each $.25 increase in fare.
Let the number of riders be a function of the fare charged. Graph the function, identify the graph of the function (line, parabola, hyperbola, or exponential), find the slope of the graph, find the price at which there will be no more riders, and the maximum number of riders possible.
The bus company has determined that even if they set the price very low, there is a maximum number of riders permitted each day. If the price is $0 (free), how many riders are permitted each day?
If the bus company sets the price too high, no one will be willing to ride the bus. Beginning at what ticket price will no one be willing to ride the bus?
Thank-you so much!
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A bus company in a small town has an average number of riders of 800 per day. The bus company charges $2.25 for a ride. They conducted a survey of their customers and found that they will lose approximately 40 customers per day for each $.25 increase in fare.
Let the number of riders be a function of the fare charged. Graph the function, identify the graph of the function (line, parabola, hyperbola, or exponential), find the slope of the graph, find the price at which there will be no more riders, and the maximum number of riders possible.
:
Let x = number of riders, y = fare amt
Let x1 = 2.25, y1 = 800
According to the problem, an increased fare of $.75,(3 ea 25 cent increases, $3)
would drop the no. of passengers to: 800 - 3(40) = 680:
Let x2 = 3, y2 = 680
:
Find the slope using the slope formula (m) = (y2-y1)/(x2-x1)
m = (680-800)/(3-2.25)
m = -120/.75
m = -160 is the slope:
:
Use the point/slope formula: y-y1 = m(x-x1)
y - 800 = -160(x - 2.25)
y - 800 = -160x + 360
y = -160x + 360 + 800
y = -160x + 1160
:
Graphing it:
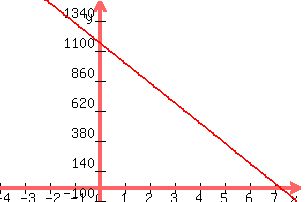
:
Obviously it is a line with a negative slope (-160), to find the value of x when
there are 0 passengers (y):
-160x + 1160 = 0
-160x = -1160
x = -1160/-160
x = +$7.25 is the fare where no one will be riding
:
Max no. of passengers would be when the fare (x) is 0. 1160 passengers, right?
y = -160(0) + 1160
:
:
The bus company has determined that even if they set the price very low, there is a maximum number of riders permitted each day. If the price is $0 (free), how many riders are permitted each day?
If the bus company sets the price too high, no one will be willing to ride the bus. Beginning at what ticket price will no one be willing to ride the bus?
;
I think we answered these last two questions.
|
|
|