SOLUTION: IS THERE A SOLUTION TO THESE PROBLEM m^2+m+1=0 3z^2+z-1=0 (7)1/2y^2-6y-13(7)1/2=0

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons -> SOLUTION: IS THERE A SOLUTION TO THESE PROBLEM m^2+m+1=0 3z^2+z-1=0 (7)1/2y^2-6y-13(7)1/2=0      Log On


   

Question 55278: IS THERE A SOLUTION TO THESE PROBLEM
m^2+m+1=0
3z^2+z-1=0
(7)1/2y^2-6y-13(7)1/2=0
Answer by funmath(2933) About Me  (Show Source):
You can put this solution on YOUR website!
IS THERE A SOLUTION TO THESE PROBLEMS?
It depends on how far you are in math. If this is not where you're at let me know.
1.) m%5E2%2Bm%2B1=0
We can use the discriminant to determine if there is a solution.
This is in standard form: highlight%28ax%5E2%2Bbx%2Bc=0%29
The Discriminant is highlight%28b%5E2-4ac%29
If the discriminant is positive, there are two real solutions. If it's a perfect square there are two rational solutions and you can find them by factoring. If it's not a perfect square, there are two irrational solutions that can only be found using athe quadratic formula.
If it's 0, there is one real solution. The qradratic equation is a perfect square trinomial and can be solved by factoring.
If it's negative, there are no real solutions, but two complex solutions. (I don't think you're that far yet, let me know if your are.)
In this case a=1, b=1, and c=1
highlight%28b%5E2-4ac%29
%281%29%5E2-4%281%29%281%29
1-4=-3 The discriminant is negative, so there are no real solutions.
:
3z%5E2%2Bz-1=0
a=3, b=1, and c=-1
highlight%28b%5E2-4ac%29
%281%29%5E2-4%283%29%28-1%29
1%2B12=13 The discriminant is positive so this has two real solutions, but you have to use the quadratic formula to find them because you can't take the squareroot of 13. If you haven't started the quadratic formula, you can't find the solution.
:
%287%291%2F2y%5E2-6y-13%287%291%2F2=0
a=7/2, b=-6, c=-13(7)/2=-91/2
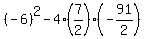
%28-6%29%5E2-4%287%2F2%29%28-91%2F2%29
36%2B2548%2F4
36%2B637=673 The discriminant is positive so there are two real solutions. But 673 is not a perfect square, so you have to use the quadratic formula to find them.
Happy Calculating!!!