Question 55150: When using the quadratic formula to solve a quadratic equation ax2 + bx + c = 0, the discriminant is b2 - 4ac. This discriminant can be positive, zero, or negative. (When the discriminant is negative, then we have the square root of a negative number. This is called an imaginary number, sqrt(-1) = i. )
Explain what the value of the discriminant means to the graph of y = ax2 + bx + c. Hint: Chose values of a, b and c to create a particular discriminant. Then, graph the corresponding equation.
Answer by funmath(2933)   (Show Source):
You can put this solution on YOUR website! When using the quadratic formula to solve a quadratic equation ax2 + bx + c = 0, the discriminant is b2 - 4ac. This discriminant can be positive, zero, or negative. (When the discriminant is negative, then we have the square root of a negative number. This is called an imaginary number, sqrt(-1) = i. )
:
Explain what the value of the discriminant means to the graph of y = ax2 + bx + c. Hint: Chose values of a, b and c to create a particular discriminant. Then, graph the corresponding equation.
:
When the discriminant is positive there are two real solutions. (Two places the graph crosses the x-axis.
has a discriminant of  1 is positive and the solution is: x={-3,-2} and the graph y=x^2+5x+6 crosses the x-axis at -3 and -2.
:
When the discriminant is 0, there is one real solution and the graph barely touches the x axis in one place.
has a discriminant of
 and the real solution is x=-2 and the graph of y=x^2+4x+4 barely touches the x axis in one place x=-2
:
When the discriminant is negative there are two imaginary solutions and the graph doesn't cross the x-axis.
has a discriminant of  and has two imaginary solutions, 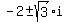 . Double check that-I didn't write it down to solve it with the quadratic equation, but you didn't ask for that. It was a freebie.
The graph looks like:
Happy Calculating!!!
|
|
|
