Question 551052: find k so thqqt the equation x2-11x+k=0 andx2-14x+2k=0 may have a common root
Found 2 solutions by oberobic, KMST:
Answer by oberobic(2304)   (Show Source):
You can put this solution on YOUR website! f(x) = x^2 -11x + k
g(x) = x^2 -14x + 2k
.
x = 0 defines the roots
But that reveals we would be looking for a point where k = 2k.
That exists only at k=0.
Given k=0, we can redefine f(x) and g(x):
f(x) = x*(x-11)
g(x) = x*(x-14)
They share the common root 0.
.
Answer by KMST(5328)  (Show Source):
You can put this solution on YOUR website! An obvious solution is  .
However,  is another solution, giving both equations,
 and 
the common root  .
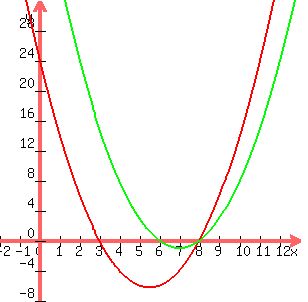
A common root would be a solution of the non-linear system of non-linear equations:
We can combine them to give
 -->  --> 
which we could use, along with the friendliest of the quadratic equations above to search for all possible solutions.
has the solutions
Combining them, we get
 -->  -->  -->  -->  --> 
So we get two answers and , and both verify.
For k=0, we get x=0/3=0.
For k=24 we get x=24/3=8.
The solutions are the (x,k) pairs (0,0) and (8,24).
|
|
|
