Question 491989: Please help me solve this quadratic equation in a step-by-step manner by completing the square :

Found 2 solutions by nerdybill, Theo:
Answer by nerdybill(7384)   (Show Source): (Show Source):
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the equation is:

it is already in standard form of ax^2 + bx + c = 0, so we are ready to find the roots using the completing the squares method.
STEP 1.
add 3 to both sides of the equation to get:

this step is necessary to move the constant term from the left side of the equation to the right side of the equation.
if there is no constant term, then this step is not necessary.
STEP 2.
divide both sides of the equation by 3 to get:
 which becomes: which becomes:

this step is necessary to make the coefficient of the x^2 term equal to 1.
if the coefficient of the x^2 term is already 1, then this step is not necessary.
STEP 3.
take 1/2 of the coefficient of the x term to get:

STEP 4.
square 1/2 of the coefficient of the x term to get:

STEP 5.
add the square of 1/2 the coefficient of the b term to the right side of the equation to get:

the reason for doing this step will be shown below after all steps have been completed and you have derived a solution to your problem.
STEP 6.
create the square root factor on the left side of the equation to get:

the square root factor will be 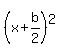 or it will be or it will be  , depending on the sign of the b term. , depending on the sign of the b term.
the  term is term is  of the b term after it has been divided by the a term. of the b term after it has been divided by the a term.
this is the term that you calculated in step 3.
you started with:

you added the c term to both sides of the equation to get:

you divided both sides of the equation by 3 to get:

you took  of the b term to get of the b term to get  . .
that's the  term we are talking about here. term we are talking about here.
as shown above, your equation becomes:

STEP 7.
take the square root of both sides of the equation to get:
x - 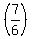 = +/- = +/- 
STEP 8.
add (7/6) to both sides of the equation to get:
x = 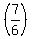 +/- +/- 
that should be your answer.
you will get:

or:

you confirm by replacing x in the original equation with these values of x. if the equation holds true, then you have a solution to the equation.
the easiest way to do this is to use your calculator to reduce the value of x to a number that you then substitute for the value of x in the equation.
your original equation is:

the values of x that are supposed to be good are:

or:

x =  becomes x = 2.70325741 becomes x = 2.70325741
replace x in the original equation with this value and you get:
 becomes: becomes:
 which becomes: which becomes:
0 = 0, confirming the value of x = 2.70325741 is good.
 becomes x = -.369924076 becomes x = -.369924076
replace x in the original equation with this value and you get:
 becomes: becomes:
 which becomes: which becomes:
0 = 0, confirming the value of x = -.369924076 is good.
both values of x are good, so you solved the quadratic equation using the completing the squares method correctly.
here's a reference that tells you how the completing the squares method works.
that's the same method we used in solving your problem.
http://www.purplemath.com/modules/sqrquad.htm
WHY YOU ADDED  TIMES THE B TERM TO BOTH SIDES OF THE EQUATION. TIMES THE B TERM TO BOTH SIDES OF THE EQUATION.
the equation you had to work with at the end of step 2 was:

you took  of the b term to get of the b term to get 
you then squared that to get 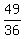 which you then added to both sides of the equation. which you then added to both sides of the equation.
if you did not do that, this is what would have happened:
you create your squaring factor by using  of the b term to get: of the b term to get:

the b term divided by 2 is used to create your squaring factor.
if you square 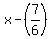 then you will get: then you will get:
 which becomes: which becomes:

the left side of your equation needs to be:
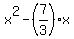
instead it became:
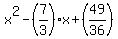
in order to remove that extra (49/36), you need to make your starting equation equal to:

this removes the extra 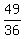 that is the result of that is the result of  . .
if you add 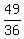 to both sides of this equation, then you get: to both sides of this equation, then you get:

that's why you added 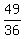 to both sides of the equation in step 5. to both sides of the equation in step 5.
|
|
|