Question 427879: What happens when the quadratic equation is no solution? For example,
x2+6x+10=0
A=1 B=6 C=10
D= b2-4ac
D=62-4(10)=-4
-4<0 no real solutions
What now?
Thank you :)
Found 2 solutions by MathLover1, richard1234:
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Solving by the Quadratic Formula
Since this formula is somewhat long and complicated, it is best to evaluate it in two smaller pieces by first evaluating the thing inside the radical,

and then put the result into the formula

The quantity
b^2-4ac
even has a name.
It is called the discriminant. And there is another advantage to computing it first. Since it is what is in the radical, it can't be negative if there are going to be solutions to the equation, because you can't take a square root of a negative number, (unless you use the imaginary numbers, and we're not yet ready for them here) so if the discriminant comes out negative, then you don't have to do any more work, and all you have to do is write "no solution" on your paper and you are done. Sometimes you can determine this quite quickly by estimating, particularly if a and c are very large and b is small.
Example
Problem: Solve the equation.

Solution:
here we have no solution because  is is  , which is very small in comparison to , which is very small in comparison to  and and  , so you don't , so you don't  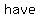 to compute the discriminant to to compute the discriminant to 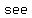 that it is going to be that it is going to be 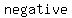 . .
Answer by richard1234(7193)   (Show Source): (Show Source):
You can put this solution on YOUR website! Then there are no real solutions. Graphically, this would mean that on the xy-plane, the quadratic would not intersect the x-axis. The quadratic does have two complex solutions, which can be shown graphically by graphing on a three-dimensional plane.
|
|
|