Question 414468: please help me find the roots, lines of symmetry, and vertex for y=-x2+5x-4
Found 3 solutions by stanbon, rfer, MathLover1:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! please help me find the roots, lines of symmetry, and vertex for
y=-x^2+5x-4
----
-x^2+5x+? = y+4+?
----
Complete the square on the x-terms:
-(x^2-5+(5/2)^2) = y+4-(5/2)^2
---
Factor:
-(x-(5/2))^2 = y + 16/4 - (25/4)
----
-(x-(5/2))^2 = y -9/4
-------
Symmetry line : x = 5/2
Vertex: (5/2 , (9/4))
----
Roots of y = -x^2+5x-4
Solve -x^2+5x-4 = 0
x^2-5x+4 = 0
(x-4)(x-1) = 0
x = 1 or x = 4
---
Cheers,
Stan H.
Answer by rfer(16322)   (Show Source): (Show Source):
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!  ....factor ....factor




This is a quadratic equation (degree of 2), so
First, find x-intercepts,
Let and solve for and solve for  : :

 ........->.... ........->.... and and
 ........->.... ........->....
So, the  (roots) are (4,0) and (1,0) (roots) are (4,0) and (1,0)
Now, find the 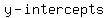 , let , let  and solve for and solve for  , ,
 , so the , so the 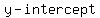 is (0,-4) is (0,-4)
The axis of  is just the average of the two is just the average of the two  , ,

So, the axis of symmetry is 
Since the sign of  is negative then this function will have a maximum. is negative then this function will have a maximum.
Now, to find it's maximum (vertex).
Formula for maximum value is 
 , ,  , ,  ( Coefficients of ( Coefficients of  ) )

this is exactly  , which is not surprising because the , which is not surprising because the 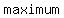 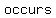 on the axis of on the axis of  . .
Now, find the  value corresponding to the value corresponding to the  value, value,
Substitute,  into the equation and solve for into the equation and solve for  , ,



Summarize:
You should have more than enough now for a graph,
 : (4,0) and (1,0) : (4,0) and (1,0)
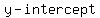 : (0,-4) : (0,-4)
maximum value (vertex) : (2.5,2.25)
axis of  : : 

|
|
|