The maximum or minimum point (vertex) of the graph of
 has x-coordinate =
has x-coordinate =  If a is a positive number, the vertex is a minimum.
If a is a negative number, the vertex is a maximum
Its y-coordinate is found by substituting the value of the x
coordinate for x into
If a is a positive number, the vertex is a minimum.
If a is a negative number, the vertex is a maximum
Its y-coordinate is found by substituting the value of the x
coordinate for x into  It's zeros are
It's zeros are
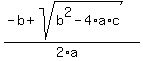 ,0)
and
,0)
and
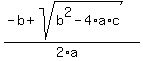 ,0)
The axis of symmetry is the vertical line which passes through the
vertex and has the equation
,0)
The axis of symmetry is the vertical line which passes through the
vertex and has the equation
 The y-intercept is (0,c)
------------------------------------
Identify the maximum or minimum (vertex), zeros, and axis of symmetry line and show the graph.
y=x^2-4x+1
a=1, b=-4, c=1
The maximum or minimum point (vertex) of the graph of
The y-intercept is (0,c)
------------------------------------
Identify the maximum or minimum (vertex), zeros, and axis of symmetry line and show the graph.
y=x^2-4x+1
a=1, b=-4, c=1
The maximum or minimum point (vertex) of the graph of

 a=1, b=-4, c=1
has x-coordinate =
a=1, b=-4, c=1
has x-coordinate =  =
= 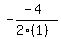 =
=  =
=  a=1 is a positive number, so the vertex is a minimum.
Its y-coordinate is found by substituting the value of the x
coordinate for x into
a=1 is a positive number, so the vertex is a minimum.
Its y-coordinate is found by substituting the value of the x
coordinate for x into  Substituting 2 for x
Substituting 2 for x



 So the y-coordinate is -3 and so the vertex has
coordinates:
(2, -3)
It's zeros are
(
So the y-coordinate is -3 and so the vertex has
coordinates:
(2, -3)
It's zeros are
(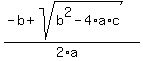 ,0)
and
(
,0)
and
(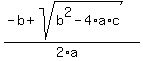 ,0)
Substituting a=1, b=-4, c=1
(
,0)
Substituting a=1, b=-4, c=1
(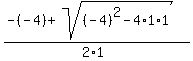 ,0)
(
,0)
(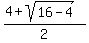 ,0)
(
,0)
(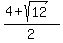 ,0)
(
,0)
(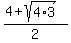 ,0)
(
,0)
(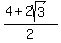 ,0)
(
,0)
(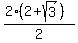 ,0)
(
,0)
(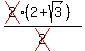 ,0)
(
,0)
(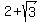 ,0)
Similarly just be changing the sign before the radical term
above, the other zero is
(
,0)
Similarly just be changing the sign before the radical term
above, the other zero is
(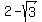 ,0)
They are approximately (.27,0) and (3.73,0)
The axis of symmetry is the vertical line which passes through the
vertex and has the equation
,0)
They are approximately (.27,0) and (3.73,0)
The axis of symmetry is the vertical line which passes through the
vertex and has the equation
 which is
which is
 We plot the vertex, the x-intercepts and the axis of symmetry (in green).
and the y-intercept is (0,c)
We plot the vertex, the x-intercepts and the axis of symmetry (in green).
and the y-intercept is (0,c)
 Then sketch in the graph:
Then sketch in the graph:
 Edwin
Edwin