Question 344391: 10y^2+11y-6
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! 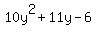 is an expression and it is a simplified expression. So I'm not sure what you have been asked to do. I am going to guess what the problem is but if I am wrong, then repost your entire problem.
My guess is that the problem is to solve the equation:
This is a quadratic equation (because of the  term). To solve quadratic equations I recommend:- Simplify each side of the equation.
- Make one side of the equation equal to zero.
- Factor the non-zero side. (If the non-zero expression does not factor, use the Quadratic Formula and skip step 4.)
- Use the Zero Product property and solve the resulting equations (which are simple equations).
Your equation is already simplified and one side is already zero. So we can go straight to step 3: Factor.
This trinomial, with the 10 in front of the squared term, is not a simple one to factor. You are looking for the right combination of factors of the 10 and factors of the -6 that will result in the 11 in the middle. Some learn to do this with a "box". If this is how you have learned it, then go ahead and use it (especially if my upcoming explanation is not clear).
Since -6 is negative, one of the factors we will use will be positive and the other factor will be negative. That means that we will be adding a positive and a negative number in order to get the 11. Thinking about how adding a positive and a negative works and thinking that we end up with a sum of positive 11, we can figure that the positive number must significantly larger (by 11 to be exact) in absolute value than the negative number. This narrows down the possibilities quite a bit.
For the factors of 10 we can use 1 and 10 or 2 and 5.
For the factors of -6 we can use -1 and 6, 1 and -6, 2 and -3, or -2 and 3.
It shouldn't take long to find the one and only combination which gives us the 11:
So our equation, in factored form, is
Now we can use the Zero Product property which says that this (or any) product can be zero only if one of the factors is zero. So
 or 
Solving these equations we get:
 or 
NOTE: Using the Quadratic Formula will result in these answers, too. But the formula can be hard to remember and even harder to work with (because of the square root and the "plus or minus"). So I recommend using it only when factoring is impossible or too difficult.) Also, factoring is so useful in so many ways in addition to solving quadratic equations that it is good to get good at it and keep in practice by using it frequently.
|
|
|
