SOLUTION: x^2 + 3/5x - 1/12 = 0

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons -> SOLUTION: x^2 + 3/5x - 1/12 = 0      Log On


   

Question 323605: x^2 + 3/5x - 1/12 = 0
Answer by JBarnum(2146) About Me  (Show Source):
You can put this solution on YOUR website!
Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 1x%5E2%2B0.6x%2B-0.0833333333333333+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%280.6%29%5E2-4%2A1%2A-0.0833333333333333=0.693333333333333.

Discriminant d=0.693333333333333 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28-0.6%2B-sqrt%28+0.693333333333333+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%280.6%29%2Bsqrt%28+0.693333333333333+%29%29%2F2%5C1+=+0.116333199893226
x%5B2%5D+=+%28-%280.6%29-sqrt%28+0.693333333333333+%29%29%2F2%5C1+=+-0.716333199893227

Quadratic expression 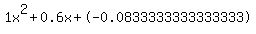1x%5E2%2B0.6x%2B-0.0833333333333333 can be factored:

Again, the answer is: 0.116333199893226, -0.716333199893227. Here's your graph: