Q.3:-Show that there is no integer a such that a^2-3a-19 is divisible by 289?
Let  We need to show that k is not an integer.
Assume, for contradiction, that it is an integer.
We need to show that k is not an integer.
Assume, for contradiction, that it is an integer.



 For
For  to have a rational solution,
the discriminant
to have a rational solution,
the discriminant  must be a perfect
square.
Here
must be a perfect
square.
Here  ,
,  ,
,  discriminant =
discriminant =  In order for this discriminant,
In order for this discriminant, 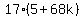 , to be a
perfect square, since it has one factor of 17, the other
factor
, to be a
perfect square, since it has one factor of 17, the other
factor  must also have a factor of 17. So there
must be an integer n such that
must also have a factor of 17. So there
must be an integer n such that



 But the right side is an integer but the left side is not.
This contradicts our assumption that the discriminant is a perfect
square.
Therefore "a" cannot be a rational number. And since "a" is
not a rational number, it certainly cannot be an integer.
Edwin
But the right side is an integer but the left side is not.
This contradicts our assumption that the discriminant is a perfect
square.
Therefore "a" cannot be a rational number. And since "a" is
not a rational number, it certainly cannot be an integer.
Edwin