Question 232486: I need help trying to figure out how to factor (using the factoring by pairs technique): x^5+x^2-4x^3-4
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! Factoring by pairs (aka factoring by grouping) is best done when the expression is all additions. Since addition is commutative and associative, an expression of all additions can be reordered and regrouped in any way you choose. So I will start be rewriting your expression as additions:
Now we'll start the factoring. To factor by pairs we must group terms into pairs which have a common factor. This may require reordering of terms. In your expression, since the first two terms have a common factor and since the last two terms also have a common factor, we will not have to reorder the terms (yet). Factoring out the GCF of each pair we get:
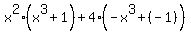
After we factor out the common factors in each pair, we now have the other factor for each pair,  for the first pair and 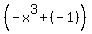 for the second pair. What we want is for these other factors to match. These do not match. But they are negatives of each other! So if we factor out a -1 from one of them they will match. (A -1 can always be factored out of any expression. So keep your eye out for this.) I'll factor out a -1 from the second "other" factor:
or
(If we had factored out -4 to begin with, instead of 4, we would have matched our "other" factors more quickly.)
If are unable to match the "other" factors, even after factoring out a -1, then we start over and try a different grouping of terms. Eventually it will either factor or you will run out of all the possible groupings, including reordering of terms, and decide that the expression will just not factor this way.
Now that our "other" factors in each group match, we can factor that factor out. I'll use color coding so you can see what's what:
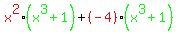
And, as always with factoring, you keep factoring (using any and all factoring techniques) until you cannot factor any further. The first factor fits the Sum of Cubes pattern,  , and the second factor fits the Difference of Squares pattern,  . Using these patterns we get:
|
|
|
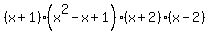
