Question 2079: The height of a object in feet at time t in seconds is h= 72t-16t^2. When does it hit the ground and what is its maximum height?
Answer by matthew_sessoms(39)   (Show Source):
You can put this solution on YOUR website! Good question.
I’m not sure what methods you are familiar with for quadratic equations. First, I will use the "complete the square method" (CTS) and then use the graphing method to prove myself.
Always write any equation in descending order. Like this,  . If you’re not familiar with the CTS method, write back and I’ll tell you.
The CTS says we must get the t^2 coefficient to be 1. We’ll do this by factoring out the -16. So we have, -16(t^2 – 9/2t) + 0
Next, we have to divide the -9/2 by 2 (which is -9/4) and then square that (which is 81/16). So far, we have 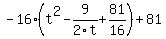 (I got the 81 by -16 * 81/16 and then changing the sign).
Now we have to factor the perfect square. We take half of -9/2, which is -9/4, and replace this with the -9/2 and 81/16, as well as reduce t^2 to t. So we have, -16(t – 9/4)^2 + 81
CTS states the equation y = a(x – h)^2 + k, where (h, k) is the maximum/minimum. Always take the opposite sign of h. Remember your h and the h in the CTS equation are not the same. Your h represents y and your t represents x. If a is negative (which yours is) then there is a max and vice versa)
So the maximum is (9/4, 81). Remember the direction of the x & y coordinate planes. You are looking for the height, so go with the y-coordinate, which is 81.
To find the time (t or x) that the object hits the ground, you must solve for t. In the original equation, we can factor out a t.
t(-16t + 72) = 0
We already know that t=0 (however, we obviously know that the object is impossible to touch the ground in 0 seconds—so just ignore this 0)
Solve for t in -16t + 72 = 0
t = -9/2
So, the ball reaches the maximum height of 81 ft. and it touches the ground in 4.5 seconds.
Here is the graph to prove my statements.
|
|
|
