Question 145458: Please find the -y intercept
x intercepts if any
vertex
and line of symetry of the following quadratics.
1.
2.
3.
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! The y intercept is at x = 0. f(0) is:
1. 12
2. 5
3. 15
1. 
| Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc) |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
The discriminant -44 is less than zero. That means that there are no solutions among real numbers.
If you are a student of advanced school algebra and are aware about imaginary numbers, read on.
In the field of imaginary numbers, the square root of -44 is + or -  . .
The solution is  , or , or
Here's your graph:
 |
2. 
| Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc) |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=16 is greater than zero. That means that there are two solutions:  . .


Quadratic expression  can be factored: can be factored:

Again, the answer is: 5, 1.
Here's your graph:
 |
3. 
| Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc) |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=4 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 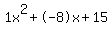 can be factored: can be factored:

Again, the answer is: 5, 3.
Here's your graph:
 |
|
|
|