SOLUTION: I was absent from school the day my class went over this and need help. The question is: Find the equation of the axis of symmetry and the coordinates of the vertex of the grap

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons -> SOLUTION: I was absent from school the day my class went over this and need help. The question is: Find the equation of the axis of symmetry and the coordinates of the vertex of the grap      Log On


   

Question 139028This question is from textbook Texas Algebra 1
: I was absent from school the day my class went over this and need help. The question is:
Find the equation of the axis of symmetry and the coordinates of the vertex of the graph of each function.
Problem 1:
+y=2x%5E2%2B4. This question is from textbook Texas Algebra 1

Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
Not sure why you have the '=0' in there. If it equals zero, then you only have two points -- no graph, no axis of symmetry, and no vertex. Setting your expression equal to zero is how you discover where the graph crosses the x-axis.

y=2x%5E2%2B4.

All parabolas can be expressed like this: y=ax%5E2%2Bbx%2Bc. In your case, the values of a, b, and c are a=2, +b=0+, and c=4.

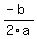The x-coordinate of the vertex is found at x=%28-b%29%2F2a, which also happens to be the equation of the axis of symmetry. The y-coordinate of the vertex is just the value of the function at the value of the x-coordinate of the vertex, in other words:

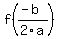(%28-b%29%2F2a,f%28%28-b%29%2F2a%29)

So step 1 is to calculate the value of 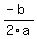%28-b%29%2F2a to get the x-coordinate of the vertex.

Step 2: substitute that value for x in your original function and do the arithmetic. The result is the y-coordinate of the vertex.

Step 3: just write x=%28-b%29%2F2a, substituting the value you calculated, to create the equation of the axis of symmetry.