Question 135067: What is the difference between domain and range? Describe a real-life situation that could be modeled by a function.
Can someone explain this so I can understand it?
Found 2 solutions by vleith, solver91311:
Answer by vleith(2983)   (Show Source):
You can put this solution on YOUR website! The domain is the set of all valid value for the 'independent' variable. The range is the set of the resulting 'dependent' variable.
So, let's say you had a function like 
Then the domain is the set of all valid values for x and the range is the values you would get for all the 'y' when you subbed in all the 'x's.
As far a a function goes, let's say you want to go to a local theme park. Tickets are $25 and parking is $10.
The total price for a family is given by  where a is the number of people in the family.
For that function the domain is all values of 'a' that are positive (no family has 0 or negative number of members).
The range is (35, 60, 85, 110, etc... like that)
Answer by solver91311(24713)  (Show Source):
You can put this solution on YOUR website! Think of a function as a machine. It looks like a little box with a slot in the top and little tray on the side. You put numbers into the slot and different (usually) numbers come out in the little tray. I say usually because if the function were f(x) = x, then you would get the same number out that you put in.
Now, if there are certain numbers that would cause the machine to malfunction, usually either because you would be trying to divide by zero or put a negative number under a radical, then you would have to put a warning sign on the box telling you not to put certain numbers into the slot.
Example:  . Clearly 2 would make the denominator go to zero, and your little machine would either melt down or blow up. So you would need a sign on it that says "WARNING: Do Not Insert the Number 2"
The domain of a function is the set of numbers that CAN go in the slot. For some functions, this set is all real numbers, as in  . For other functions, you may have to exclude certain discrete numbers, as in  where either  or  would damage the machine. Still other functions might require you to exclude entire ranges of numbers in order to be defined over the real numbers, example:  . Here, x must be greater than or equal to 2 so that the value under the radical is never negative.
The range of a function is the set of numbers that comes out in the little tray. If you took your machine and put in every possible number in the domain, the range would be the set of numbers that came out the other end.
Let's look at some examples:
: When x gets close to 2, the function gets very large. Once you get to calculus, you will prove that  or  depending on whether you approach 2 from the right or the left. Any x on the interval [0,2) gives a negative result, everything else (except 2) gives a positive result. That covers the entire set of real numbers. So the range is all reals.
: This is a parabola that is concave up, so the vertex is a minimum. The vertex is at ( , ), so the range is [ , )
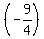Hope that helps.
John
|
|
|
