Question 119027This question is from textbook U of Phoenix elementry and intermediate algebra
: I know its got to be simple, but I just don't understand quadratic equations. 12x^+5x-3=0 ^=squared
This question is from textbook U of Phoenix elementry and intermediate algebra
Found 2 solutions by stanbon, solver91311:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! 12x^2+5x-3=0
--------------
Solved by graphing:
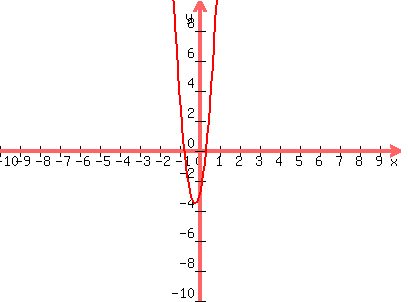
----------------
Solved by factoring:
12x^2+9x-4x-3=0
3x(4x+3)-(4x+3)=0
(4x+3)(3x-1)=0
4x+3=0 or 3x-1=0
x = -3/4 or x = 1/3
-----------------------
Solved by the quadratic formula:
x = [-5 +- sqrt(5^2-4*12*-3)]/(2*12)
x = [-5 +- sqrt(169)]/24
x = [-5 +- 13]/24
x = [-5+13]/24 or x = [-5-13]/24
x = 1/3 or x = -3/4
===========================
Cheers,
Stan H.
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
This particular quadratic is factorable, meaning that the roots of the equation are rational numbers, although this one takes a bit of work to find the factors.
A quicker method would be to use the quadratic formula and work backwards to find the factors. Here's the quadratic formula:
 , where a is the coefficient on the , where a is the coefficient on the  term, b is the coefficient on the term, b is the coefficient on the  term, and c is the constant. term, and c is the constant.
In this problem:
 . Now we are certain that the roots of the equation will be rational because 169 is a perfect square, namely . Now we are certain that the roots of the equation will be rational because 169 is a perfect square, namely  . .
Now our two answers will be  and and  . .
Since  , we can say , we can say  , and since , and since  we can say we can say  . These are the two factors of . These are the two factors of 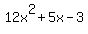 , as you will see if you use FOIL to multiply , as you will see if you use FOIL to multiply 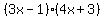 . If either one of those factors is equal to zero, the entire expression is equal to zero. . If either one of those factors is equal to zero, the entire expression is equal to zero.
Perhaps it bothers you that there are two answers. Take a look at a graph of the function  . .

See where the graph crosses the x-axis at two points? Each of these points is a zero of the function  or a root of the equation or a root of the equation  . .
Hope this helps,
John
|
|
|