Question 1165819: Mr. Lim orders chairs from a factory to sell. When he orders a batch of x chairs, the cost of each chair, $y is given by y = x2 - 14x + 80.
a. Find x such that the cost of each chair is the same as when Mr. Lim
ordered 5 chairs.
b. Find the number of chairs in a batch he needs to orders such that the cost
per chair is less than $45.
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52784)   (Show Source):
You can put this solution on YOUR website! .
Mr. Lim orders chairs from a factory to sell. When he orders a batch of x chairs,
the cost of each chair, $y is given by y = x2 - 14x + 80.
(a) Find x such that the cost of each chair is the same as when Mr. Lim
ordered 5 chairs.
(b) Find the number of chairs in a batch he needs to orders such that the cost
per chair is less than $45.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
(a) If he orders 5 chairs, the cost of each chair is
5^2 - 14*5 + 80 = 35 dollars.
To find x, we should solve this quadratic equation
x^2 - 14x + 80 = 35.
This equation is the same as
x^2 - 14x + 80 - 35 = 0,
x^2 - 14x + 45 = 0,
(x-5)*(x-9) = 0 (after factoring).
One root is 5 chairs (the value we started with).
The other root is 9, which is the ANSWER to question (a).
(b) To answer (b), we should solve this inequality
x^2 - 14x + 80 <= 45.
Transform and simplify it
x^2 - 14x + 80 - 45 <= 0,
x^2 - 14x + 35 <= 0,
Apply the quadratic formula to find the roots.
The roots are  =  .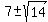
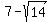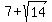So, one root is  = 3.26 (approx.) and another root is  = 10.74 (approx.)
Function x^2 - 14x + 35 is negative between the roots.
Since we are interested to know integer values of x, they are between 4 and 10 inclusive.
So, the ANSWER to question (b) is "integer numbers between 4 and 10 inclusive".
Solved.
Answer by greenestamps(13200)  (Show Source):
|
|
|
