SOLUTION: factor this quadratic equation 30(p^2-1)=11p

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons -> SOLUTION: factor this quadratic equation 30(p^2-1)=11p      Log On


   

Question 1163336: factor this quadratic equation
30(p^2-1)=11p
Found 4 solutions by Alan3354, Theo, ikleyn, greenestamps:
Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
factor this quadratic equation
30(p^2-1)=11p
---------------
Equations are solved, not factored.

Answer by Theo(13342) About Me  (Show Source):
You can put this solution on YOUR website!
your equation is 30 * (p^2 - 1) = 11 * p
simplify to get:
30 * p^2 - 30 = 11 * p
subtract 11 * p from both sides of the equation to get:
30 * p^2 - 11 * p - 30 = 0
factor this quadratic equation to get:
p = 1.2 or p = -.83333333......
when p = 1.2, the equation becomes:
30 * (1.2^2 - 1) = 11 * 1.2
this results in 13.2 = 13.2 which is true.
when p = -.83333333......, the equation becomes:
30 * ((-.83333333......)^2 - 1) = 11 * (-.83333333......)
this results in -9.1666666666...... = -9.1666666666...... which is true.
solution is confirmed to be good.
your values for p are:
p = 1.2 or p = -.83333333......










Answer by ikleyn(52775) About Me  (Show Source):
You can put this solution on YOUR website!
.

    30*(p^2-1) = 11p


This equation is EQUIVALENT to this 


    30p%5E2+-+11p+-+30 = 0.


Complete the square, step by step


    30p%5E2+-+11p = 30


    p%5E2+-+%2811%2F30%29p = 1


    p%5E2+-+2%2A%2811%2F60%29p+%2B+%2811%2F60%29%5E2 = 1+%2B+%2811%2F60%29%5E2


    %28p-11%2F60%29%5E2 = 1+%2B+121%2F3600


    %28p-11%2F60%29%5E2 = 3721%2F3600


    p+-+11%2F60 = +/- sqrt%283721%2F3600%29


    p-11%2F60 = +/- 61%2F60


    p = 11%2F60 +/- 61%2F60


The roots are  p%5B1%5D = 11%2F60+%2B+61%2F60 = 72%2F60 = 6%2F5  and

               p%5B2%5D = 11%2F60+-+61%2F60 = - 50%2F60 = - 5%2F6.


Hence, the polynomial  30p%5E2+-+11p+-+30  can be factored in this way


    30p%5E2+-+11p+-+30 = 30%2A%28p-p%5B1%5D%29%2A%28p-p%5B2%5D%29 = 30%2A%28p-6%2F5%29%2A%28p%2B5%2F6%29 = %285p-6%29%2A%286p%2B5%29.


It is the factorization the problem wants from you.

Solved.



Answer by greenestamps(13198) About Me  (Show Source):
You can put this solution on YOUR website!


The response from tutor @Theo show you a path to the answer; but it doesn't show you HOW to factor the quadratic. Since your question was how to factor the quadratic, that response is not of much use.

The response from tutor @ikleyn shows you a path that always works, by completing the square.

There are numerous other methods for finding the answer, including some techniques for actually doing the factoring.

But if you are going to use completing the square to find the factorization, you might as well just use the quadratic formula. The roots are

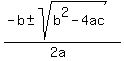
%28-b+%2B-+sqrt%28b%5E2-4ac%29%29%2F%282a%29

Plugging in a=30, b=-11, and c=-30...

%2811+%2B-+sqrt%28121%2B3600%29%29%2F60
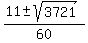
%2811%2B-sqrt%283721%29%29%2F60
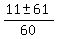
%2811+%2B-+61%29%2F60
72%2F60+=+6%2F5 or -50%2F60+=+-5%2F6

With roots 6/5 and -5/6, the quadratic expression is

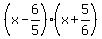
%28x-6%2F5%29%28x%2B5%2F6%29
or
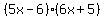
%285x-6%29%286x%2B5%29

For actually performing the factorization, here is one popular technique:

(1) Divide the leading coefficient by 30 (to make it equal to 1) and multiply the constant by that same 30 to get a new quadratic: x^2-11x-900
(2) Factor this by the standard method -- finding two numbers whose product is 900 and whose difference is 11; those numbers (not easy to find) are 25 and 36
(3) Write the factorization as (x+25)(x-36) to give the roots -25 and +36
(4) Divide each root by 30 (as used in step 1) to get the roots -5/6 and +6/5
(5) Use those roots to write the factorization (6x+5)(5x-6)

And finally a good old-fashioned method for factoring the quadratic....

The factorization is going to be of the form

(ax+b)(cx-d)

The obvious conditions are
(1) the product of a and c is 30
(2) the product of b and d is 30

With only those conditions, there are a huge number of possible factorizations. However, there are additional conditions that greatly limit the number of possibilities.
(3) a and b are relatively prime
(4) c and d are relatively prime

If either of (3) or (4) were violated, then one of the linear factors would have a common factor; and that would mean the original quadratic would have a common factor. Since the original quadratic does not have a common factor, conditions (3) and (4) are required.

It doesn't take too long now to list all the possible factorizations and to find the one that gives the correct middle term.

(30x+1)(x-30) no
(15x+2)(2x-15) no
(10x+3)(3x-10) no
(6x+5)(5x-6) YES