Question 1156645: Solve. Use a graphing calculator if necessary. See Examples 9 - 11. (Objective 8)
From the top of the building, a ball is thrown straight up with an initial velocity of 64 feet per second. The equation
s = −16t2 + 64t + 80
gives the height s of the ball t seconds after it is thrown. Find the maximum height (in feet) reached by the ball and the time (in seconds) it takes for the ball to hit the ground. (Hint: Let s = 0 and solve for t.)
80 ft
A rectangular building is 80 ft tall.
A curved path starts at the top-right side of the building and goes up and to the right past the right edge of the building. The path gets less steep as it reaches a high point, and then it goes down and to the right, getting steeper as it goes.
The ball is at the end of the path midway between the top of the building and the ground, and its height above the ground is labeled s.
A vertical dashed line starts at the ball and goes down to touch the ground.
The maximum height reached by the ball is-
feet. The ball hits the ground after-
seconds.
Answer by ikleyn(52777)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let me start explaining DEFICIENCIES in your post and in your knowledge.
At the beginning, the post says that the ball is thrown STRAIGHT UP with the velocity of 64 ft per second.
It exactly corresponds to the equation for the height.
But then you start describing the parabolic trajectory.
In this problem, THERE IS NO parabolic trajectory in space: there is ONLY the move VERTICALLY up
and then VERTICALLY dawn.
And the reasonable assumption is that the person is standing near the edge of the roof.
After this explanation, I am ready to present the solution.
Solution
The function H(t) = -16t^2 + 64t + 80 is a quadratic function, whose plot is a parabola opened down.
This quadratic function has the maximum at the value of its argument t =  , where "a" is the coefficient at t^2
and "b" is the coefficient at t.
In your case, a= -16, b= 64, so the function gets the maximum at t = , where "a" is the coefficient at t^2
and "b" is the coefficient at t.
In your case, a= -16, b= 64, so the function gets the maximum at t = 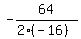 = 2.
So, the ball gets the maximum height 2 seconds after is is thrown straight up.
To calculate the maximum height, substitute t= 2 seconds into the given formula
H(t) = -16*2^2 + 64*2 + 80 = 144 feet.
Now the last question: when the ball hits the ground.
For it, you need to equate H(t) to zero, which is the ground level
H(t) = 0, or -16*t^2 + 64t + 80 =0.
Simplify the equation
16t^2 - 64t - 80 = 0
cancel the common factor 16
t^2 - 4t - 5 = 0
and factor the left side
(t-5)*(t+1) = 0.
The only positive root t= 5 is the solution. The ball will hit the ground in 5 seconds. = 2.
So, the ball gets the maximum height 2 seconds after is is thrown straight up.
To calculate the maximum height, substitute t= 2 seconds into the given formula
H(t) = -16*2^2 + 64*2 + 80 = 144 feet.
Now the last question: when the ball hits the ground.
For it, you need to equate H(t) to zero, which is the ground level
H(t) = 0, or -16*t^2 + 64t + 80 =0.
Simplify the equation
16t^2 - 64t - 80 = 0
cancel the common factor 16
t^2 - 4t - 5 = 0
and factor the left side
(t-5)*(t+1) = 0.
The only positive root t= 5 is the solution. The ball will hit the ground in 5 seconds.
Solved (with complete explanations).
----------------
On finding the maximum/minimum of a quadratic function, see the lessons
- HOW TO complete the square to find the minimum/maximum of a quadratic function
- Briefly on finding the minimum/maximum of a quadratic function
- HOW TO complete the square to find the vertex of a parabola
- Briefly on finding the vertex of a parabola
in this site.
On solving similar problems to yours in this post, see the lessons
- Problem on a projectile moving vertically up and down
- Problem on an arrow shot vertically upward
- Problem on a ball thrown vertically up from the top of a tower
- Problem on a toy rocket launched vertically up from a tall platform
in this site.
----------------
Notice that you came to the forum without having right conceptions,
and you got absolutely full and clear solution, explanation and instructions.
And you got the reading to wide your horizon.
|
|
|